【摘要】：设有无限大的等厚弹性层,其重度为w,在下面受完全约束,在上面受均布压力p,见图11.1。由于对称,试假设图11.1半无限体全界面受均匀压力这样就得到可见用位移表示的平衡方程(3.1)中的前两式自然满足,而第3式成为简化以后得积分以后得其中的A和B是任意常数。最后得应力分量的解答令p=0便得半无限体的自重应力场将式换为柱坐标仍为相同形式ν/(1-ν)为侧压系数,当ν=0时,无侧胀变形和侧压力,物态呈刚性。
设有无限大的等厚弹性层,其重度为w,在下面受完全约束,在上面受均布压力p,见图11.1。以上面为xy面,z轴铅直向下。这样,体力分量就是X=0,Y=0,Z=p。
平坦的海床、平坦而宽阔的湖基的应力场是此种状态。
由于对称(任一铅直平面都是对称面),试假设
图11.1 半无限体全界面受均匀压力
这样就得到
可见用位移表示的平衡方程(3.1)中的前两式自然满足,而第3式成为
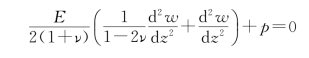
简化以后得
积分以后得
(www.xing528.com)
其中的A和B是任意常数。
现在,试根据边界条件来决定常数A和B。将几何方程式(2.2)代入物理方程式(2.6)后,再将以上的结果代入,得
将σz=wz代入,得wA=p,即A=p/w。最后得应力分量的解答
令p=0便得半无限体的自重应力场
将式(11.3)换为柱坐标仍为相同形式
ν/(1-ν)为侧压系数,当ν=0时,无侧胀变形和侧压力,物态呈刚性。当ν=0.5这个极限值时,为静水式压力各向相等,物态呈液态。
回头来看上面的结果,是在认定水平位移为零的条件下所得。这个假定是正确的,因为不仅对称,更因横向的长程不变力,故可将无限体看成是一些竖条组成,则这些竖条在自重作用下,各具相同的侧膨胀性同时也具相同的抵制侧胀力,结果只能是只有侧压力而无侧向变形,位移只能是如同一些水平叠置板整体平行下移,也就没有剪位移和剪应力。既有此认定,只需取一胡克定律式
令εx=0,σx=σy,便可得到前面的结果。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
