泛回转体的通解-空间轴对称数学力学

全空间轴对称回转体课题,用柱坐标系来表述(图8.1),会更为方便和简明。由于轴对称,应力和位移分量与极角无关,相对通常的那些基本方程,这里会明显减少。

图8.1　无限体中圆柱孔局部

平衡方程为

几何方程为

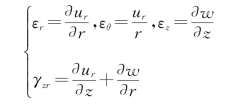
变形连续方程为

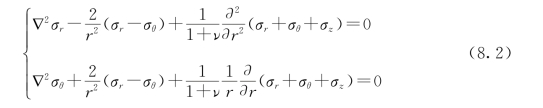
其中

为柱坐标中的拉普拉斯算子。

胡克定律为

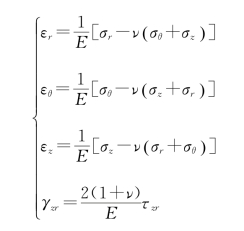
应力函数φ表达的应力、位移分量为

式中应力函数φ需满足如下的双调和方程

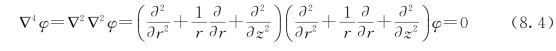
将式(8.3)代入平衡方程式(8.1)能够满足,代入变形连续方程式(8.2)可见,只要φ满足双调和方程式(8.4),式(8.2)便可满足。为寻定适合的φ,由式(8.4)试取如下方程

用分离变量法求解式(8.5),令

其中,f(r)仅为坐标r的函数,λ为实参数。将式(8.6)代入式(8.5)得到常微分方程

在式(8.7)中令ρ=λr,则化为

为获得方程(8.8)的解,试看关于复变量ξ的标准型贝塞尔方程

式中η为复常数,通常称为贝塞尔方程或贝塞尔函数的“阶”(亦有称“标值”的)。已经证明,式(8.9)可由如下两两线性无关的特殊函数的线性组合构成通解。

(www.xing528.com)

其中

Jη(ξ),Yη(ξ)分别称为第一、第二类η阶贝塞尔函数;(ξ),(ξ)分别称为第一、第二类η阶亨克尔函数。且当ξ足够大时,亨克尔函数具有简单的渐近式。

现将式(8.9)作ξ=iρ的变量替换,则式(8.9)可化为

式(8.10)相对于式(8.9)称为η阶“变形”贝塞尔方程。此时ρ为复变量。显然只需将式(8.9)的那些解组作ξ=iρ的变量替换后,即为式(8.10)的解组,取Jη(iρ),(iρ),对于这个解组乘以如下的复常数后当然亦是式(8.10)的解组

且当-π＜argρ＜时,它们是全纯函数。argρ为映射旋转角。

以上构成Iη(ρ)、Kη(ρ)作为式(8.10)的解的目的在于,当η为整数及ρ为实数时,它们均为实数,即式(8.10)的解为实数。Iη(ρ)、Kη(ρ)分别称为第一、第二类η阶变形贝塞尔函数。当ρ为实数时,它们又称为纯虚数贝塞尔函数。

Iη(ρ)、Kη(ρ)的级数表达式之一为

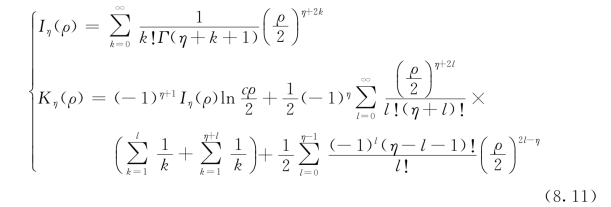
其中,欧拉常数c=0.57721566490…伽马函数,η=0,1,2,…即η+1是自然数。

Iη(ρ),Kη(ρ)具有如下的循环关系式

当|ρ|充分大时,Iη(ρ),Kη(ρ)的渐近展开式为

其中

η如前为任意复常数,ρ若为实数时,(ρ)1/2取正值。

现在回过头来看式(8.8),如果在式(8.10)中令ρ=λr为实数及η为常数后,对比式(8.8)和式(8.10)知,式(8.8)只是当式(8.10)中η=0时的特例,而式(8.10)只不过是标准型贝塞尔方程式(8.9)的变形,因此式(8.8)的通解为

在式(8.11)～式(8.14)中,当ρ=λr为实变数即λ为实数时,关系亦成立,在此也适用。由式(8.11),当ρ→∞时有

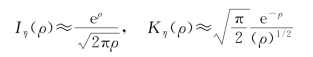
即当ρ→∞亦即r→∞时,Iη(ρ)→∞为无界,见图8.2,Kη(ρ)→∞为有界,见图8.3。为使解答有界,Iη(ρ)被用来求解圆柱体问题;而当考虑r≥a的圆柱孔外区域时,为使式(8.8)的解答式(8.15)为有界,则式(8.15)只能取c2K0(ρ)。

图8.2　Iη(ρ)曲线

图8.3　Kη(ρ)曲线