设有两个弹性体都是圆球体,其半径分别为R1及R2,见图7.1。当没有压力作用时,两球体仅在一点O接触。设两球体表面上距公共法线为r的点M1及点M2,它们距公共切面的距离分别为z1及z2,则由几何关系有

图7.1 两球相互挤压
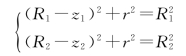
由此可以得出
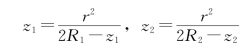
如果M1及M2离接触点O很近,则z1远小于2R1,z2远小于2R2,可近似为
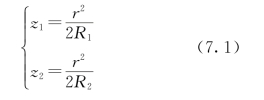
而M1与M2之间的距离为
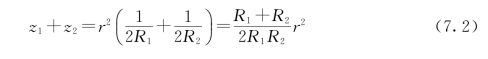
当两球体以某一力P相压时,在接触点附近将发生局部形变而出现一个边界为半径为a的圆形接触面。由于接触面的边界半径总是远小于R1及R2,故可用半无限体受集中力来分析此种局部形变。命M1沿方向z1的位移及M2沿方向z2的位移分别为w1及w2,并命轴z1上及轴z2上距点O较远处的两点相互趋近的距离为δ,则M1与M2之间的距离缩短为δ-(w1+w2)。这里所谓距点O较远处,是指该处的形变已经可以略去不计。假定在发生局部变形后,M1及M2成为接触面上的同一点M,则由几何关系有
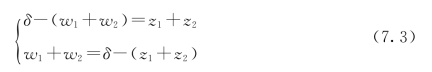
并通过式(7.2)得出

如果用图7.2中的圆表示接触面,而点M表示下面的球体在接触面上的一点(即未变形以前的M1),则该点的位移为

式中ν1及E1为下面球体的弹性常数,而积分应包括整个接触面。
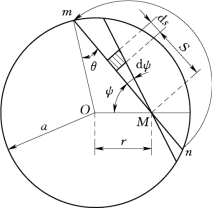
图7.2 接触面上点M的位移积分
对于上面的球体,也可以写出相似的表达式。于是得到
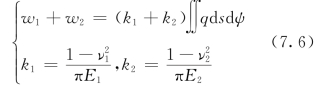
并由式(7.6)及式(7.4)得到
![]()
现在要找出压力q的分布规律,使式(7.7)可以满足。
赫兹指出,如果在接触面的边界圆上作半圆球面,而用它在各点的高度代表压力q在各点处的大小,则式(7.7)可以满足,证明如下。命q0为半圆球面在O点处的高度,亦即q的最大值,则表示压力大小的比例尺的因子为q0/a。沿着通过点M的弦mn,压力的变化如图7.2所示的虚线半圆。因此,沿着弦mn的积分为(https://www.xing528.com)
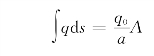
其中A为该半圆的面积,即![]() 。代入式(7.7),得
。代入式(7.7),得
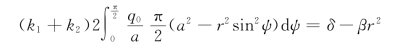
积分以后得
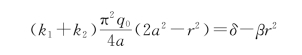
为了这一条件在r为任何值时都能满足,可以取两边的常数项相等,r2的系数也相等,即
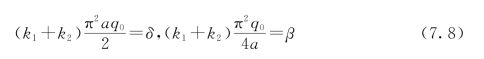
这样,式(7.7)也就可以满足。
为了得到最大压力q0,只需命上述半圆球的体积等于总的压力P,即
![]()
由此得到最大压力

它等于平均压力P/πa2的1.5倍。
将式(7.4)的第2式及式(7.9)代入式(7.8)中,求解a和δ,即得
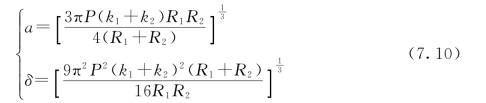
现设球1的半径R1=∞,球2取E=∞,有k2=0,则式(7.10)变为
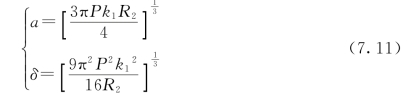
式(7.11)为刚性球体贯压半无限体边界平面所产生的球冠状变形的参数,δ为挤压方向最大变形,球冠高为
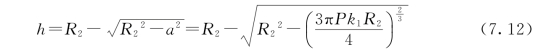
由式(7.12)看到,δ与a随k1的增大即E1的减小而增大;δ随R2的增大而减小;a随R2的增大而增大;这些都是合理而易理解的。
需要说明的是,球冠状变形未能反映全部变形。在接触边界圆外还会有变形,见图7.3。
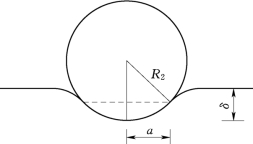
图7.3 半无限体界面球冠状变形
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




