【摘要】：设方程的摩擦力为Coulomb摩擦力，并假设机械系统的初始摩擦力较大，随系统的磨合逐渐变小。该结果是控制取F+x时获得的。图7-5 基于传统摩擦模型补偿的主动控制图图7-6是系统x和的时间响应曲线以及相平面曲线。这个例子显示了模糊神经网络系统的自适应特性的重要性，它随着摩擦环境改变而进行动态调整，该控制器短时间内就能消除摩擦诱发的振动。图7-6 基于模糊神经网络补偿的主动控制图
在这个例子中，我们验证模糊神经网络系统的建模的自适应特性。设方程（7-46）的摩擦力为Coulomb摩擦力，并假设机械系统的初始摩擦力较大，随系统的磨合逐渐变小。这一物理现象在仿真过程如下：设方程（7-11）中的初始值为0≤t<100，Fc=0.70FN；经过100s后变成100≤t<200，Fc=0.60FN，；最后阶段取200≤t≤300，Fc=0.50FN。在这个例子中取k=763N/m。
图7-5是系统x和x·的时间响应曲线以及相平面曲线。该结果是控制取
F+x时获得的。其中控制器中的摩擦力始终为F=0.70FNsgn（v）。这个例子说明，如果用传统的摩擦力模型进行补偿控制时，控制器的摩擦力如果不随实际摩擦力的改变而改变，该控制器短时间内很难消除摩擦诱发的振动。
图7-5 基于传统摩擦模型补偿的主动控制图(www.xing528.com)
图7-6是系统x和
的时间响应曲线以及相平面曲线。该结果是控制取
F+x时获得的。其中控制器中的
是模糊神经网络系统式（7-37）。这个例子显示了模糊神经网络系统的自适应特性的重要性，它随着摩擦环境改变而进行动态调整，该控制器短时间内就能消除摩擦诱发的振动。
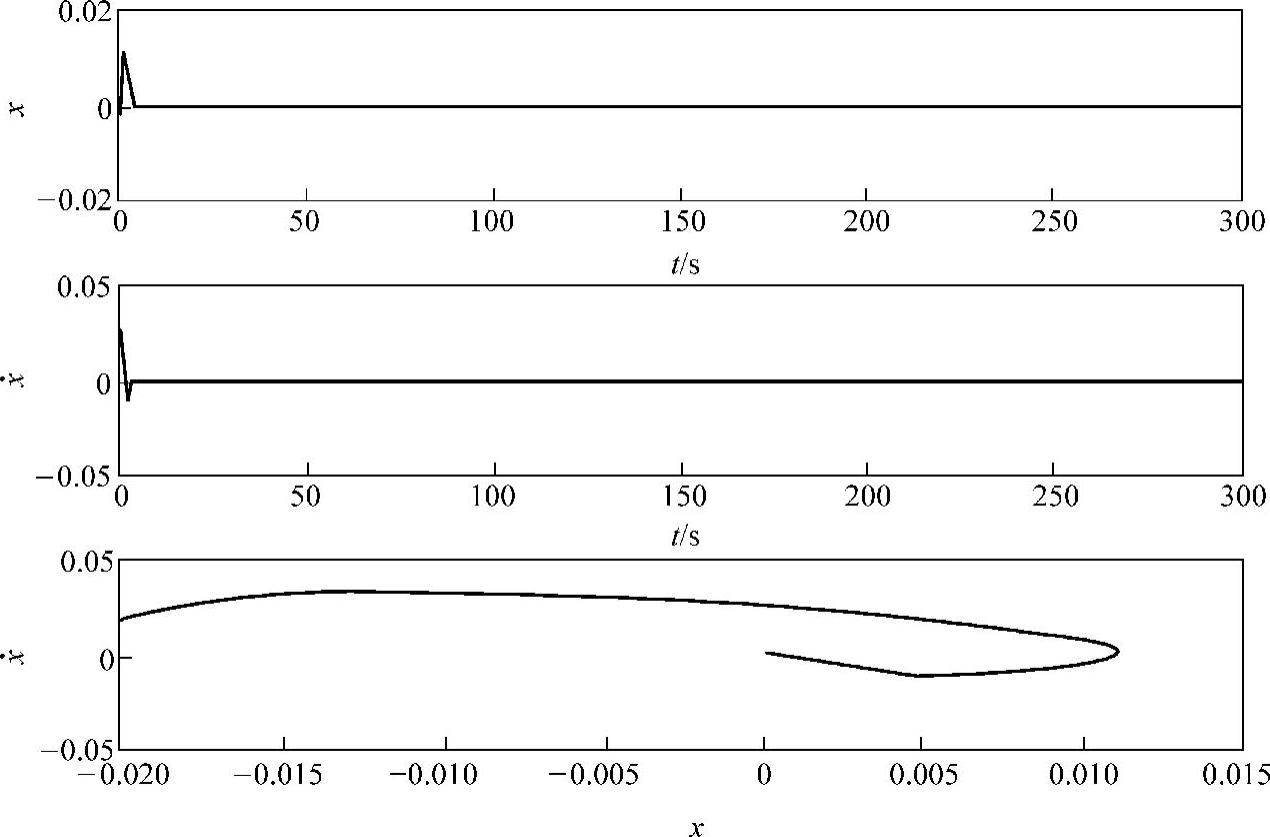
图7-6 基于模糊神经网络补偿的主动控制图
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
