若方程(7-4)中的摩擦力F和x(t)已知,可采用基于摩擦模型补偿的PD主动控制,也就是如下方程
式中e=xm-x;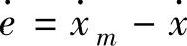 ;
;
xm——已知的系统期望输出;kp和kd——分别表示比例和微分系数。
把方程(7-27)代入方程(7-4)可得如下动态误差方程
由于在定位调节中的平衡位置参考输入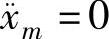 ,方程(7-28)可以写成如下方程
,方程(7-28)可以写成如下方程
显然,如果取向量k=(kd,kp)T使H(s)=s2+kds+kp为Hurwitz,则有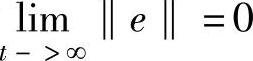 。
。
在实际工程中,位移x是可以检测到的,但摩擦力F很难精确检测或建模得到。对摩擦项F来说,由于建立精确动态摩擦模型的高难性,获到精确算法方程(7-27)是不可能的。为此,用前文的模糊系统替代方程(7-27)中的摩擦项可得
式中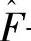 ——前文提到的模糊系统。把方程(7-30)代入方程(7-4)可得如下动态误差方程
——前文提到的模糊系统。把方程(7-30)代入方程(7-4)可得如下动态误差方程
定义最优参数向量为
式中Ωw——w的界。
那么最小逼近误差可表示如下方程
由方程(7-26)和方程(7-33),知方程(7-31)可写成如下
式中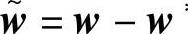 ∗。
∗。
方程(7-34)也等价如下形式(https://www.xing528.com)
式中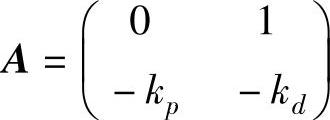
定理1.如果采用式(7-36)和式(7-37)作为主动控制器,其中自适应参数由式(7-38)在线调节
式中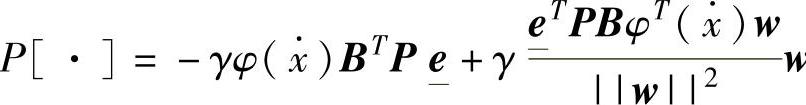 ,是投影算子。
,是投影算子。
正定解P>0满足下面的李雅普诺夫方程
ATP+PA=-Q(7-39)那么,可得到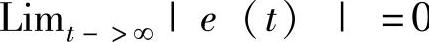 。证明:取Lyapunov函数为
。证明:取Lyapunov函数为
求V沿方程(7-40)的微分,可推出
因为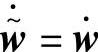 ,并结合式(7-35)可得
,并结合式(7-35)可得
由方程(7-38)和方程(7-39),上面方程对消一部分后可得到
因此,可以得到下面不等式
式中 λmin(Q)——Q的最小特征值。
对上式两边积分并取λmin(Q)>1,可以得到
如果ε∈L2,可得到e∈L2。由于方程(7-35)右边的所有变量是有界的,也就是e·(t)∈L¥。由Barbalat引理[15]可知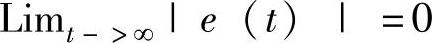 。
。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




