摩擦模型建立及控制补偿方法

神经网络具有并行计算、分布式信息存储、容错能力强，及具备自适应学习功能等一系列优点。但神经网络不适合于表达基于规则的知识，因此在对神经网络进行训练时，由于不能很好利用已有的经验知识，常常只能将初始权值取为零或随机数，从而增加了网络的训练时间或陷入非要求的局部极值。模糊逻辑也是一种处理不确定性和非线性以及其他不适定性问题的有力工具。它比较适于表示那些模糊或定性的知识，其推理方式比较类似于人的思维模式。但是一般说来它不容易实现自适应学习的功能。若将模糊逻辑与神经网络适当地结合起来，吸取两者的长处，则可组成比单纯的神经网络或模糊逻辑性能更好的系统。

模糊模型的表示方法主要有两种：一种是模糊规则后件为输出量的一个模糊集合，如NB、PB等；另一种是模糊规则后件为输入语言变量的函数，典型的情况是输入变量的线性组合。由于该模型表示是Takagi和Sugeno首先提出的，因此通常称之为模糊系统的T-S模糊模型[13]。针对摩擦具体问题，我们构造下面类似T-S模型的模糊语句如下

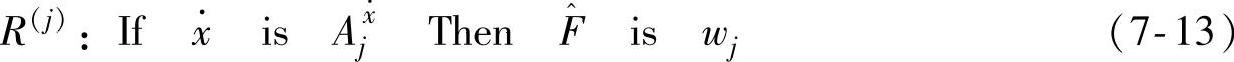
式中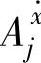——输入变量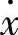的模糊集合；

w_j——第j条规则对应的输出。

根据上面给出的模糊语句，可设计出如图7-4所示的3层模糊神经网络结构[14]。第一层（输入层）：该层由单个结点构成，该结点直接与输入变量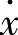相连接，它起着将输入值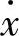传送到下一层的作用，即

第二层（隶属度函数层）：该层由N个结点构成，每个结点代表输入变量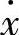的一个语言变量值，如A₁、A₂等。它的作用是计算输入分量属于各语言变量值模糊集合的隶属度函数，即

式中_μ——隶属度函数，这里采用高斯型函数。

第三层（输出层）：该层由单个结点构成，该结点直接与输出变量F^相连接，它计算系统总的输出量，即

式中w_j——加权因子。

在完成上面的模糊神经网络设计后，将用下面的数据挖掘技术设计加权因子w_j的初始值。假定通过实验或摩擦模型获得下面的实验数据对

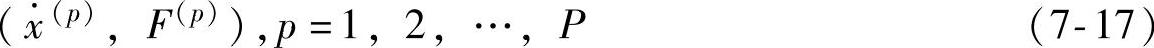
式中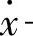——速度；

F——摩擦力。

步骤1：输入输出变量的模糊区间划分

由前面的摩擦模型可知摩擦力是速度的函数，即摩擦力随速度的变化而变化。故把速度作为模糊系统的前提变量，而把摩擦力作为结论变量。设输入变量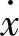域值区间取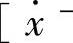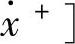，，在此域值区间取模糊集合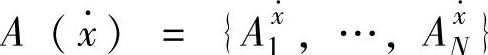，隶属度函数取高斯函数。另设输出变量F域值区间取[F^-，F⁺]，在此域值区间取模糊集合B（F）={BF1，…，BMF}，隶属度函数取三角型函数。

步骤2：关系数据库转换为模糊型关系数据库(www.xing528.com)

在摩擦的普通型关系数据库中，设T_L1表示一个普通型关系数据库，t_p表示T_L1的第p个元组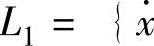，.F}表示属性集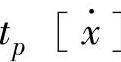，和t_p[F]分别表示属性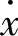和F在第p个元组上的值

T_L1={t₁，…，tp，…，tp}（7^-18）

在摩擦的模糊型关系数据库中，设T_L2表示一个模糊型关系数据库，μ（t_p）表示T_L2的第p个元组，L₂={A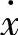（）∪B（F）}表示属性集，μ（t_p）表示t_p模糊化后的隶属度值。至此，将TL₁^一个普通型关系数据库转化为模糊型关系数据库T_L2，即

T_L2={μ（t₁），…，μ（t_p），…，μ（t_p）}（7-19）

步骤3：计算摩擦模糊规则的支持度

从数据挖掘的角度看，如果一条模糊规则有实际意义，它必须具有足够的支持度，它反映了样本元组对该条规则的支持程度.现定义支持度如下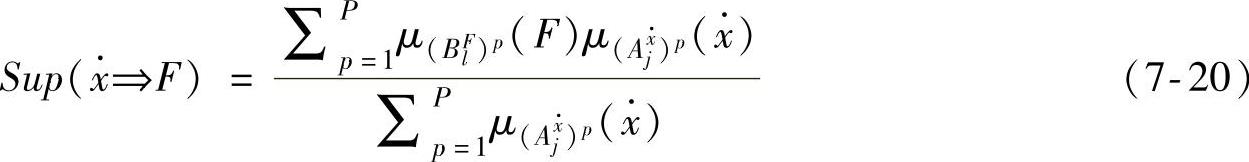为了简化计算，也可以用下式计算支持度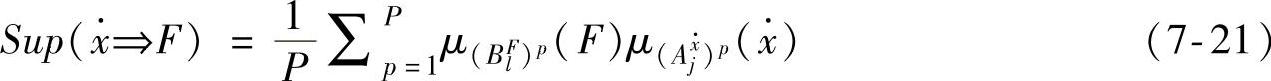

步骤4：创建完备的摩擦模糊规则库

首先，算法要保证由前提变量构成的每个模糊子空间都能被遍历。其次，结论变量在模糊子空间选用哪个模糊集，由规则的最大支持度决定。算法的主要步骤如第2章所示，通过上面的遍历产生了完备的模糊规则库。我们用一个简单例子说明此过程。设前提变量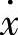和结论变量F的模糊集合分别为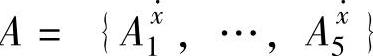和B={B^F₁，…，B₅^F}。对于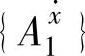，我们首先分别计算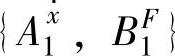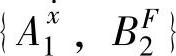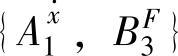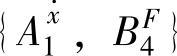，，，和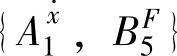的支持度，然后结论变量F最终选择的模糊集由最大支持度决定。对于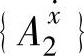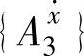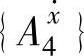，，和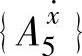重复上面的过程。由这些规则构成了所有模糊规则的一个子空间，该子空间是最后选择的模糊规则库。

步骤5：初始化模型参数

为了得到模糊神经网络的初始权值，基于最大支持度原则，取下面的摩擦模糊规则进行模糊神经网络建模

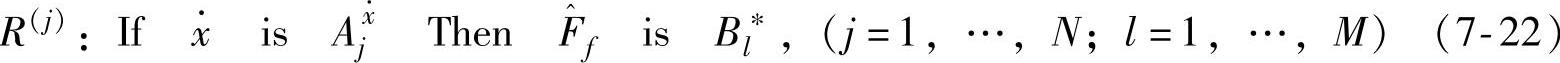
上面的模糊规则中的B_l∗通过下面的准则得到，也就是在M个模糊子集中B₁，…，B_M中通过式（7-23）找到B_l∗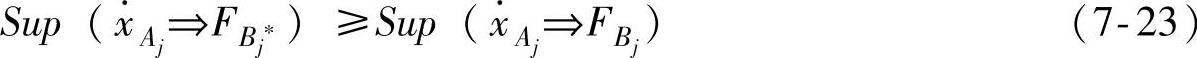通过比较式（7-13）和式（7-22），可以得到下面的初始权值

式中 F——隶属度函数μ_Bl∗（F）取得最大值的点。

定义模糊神经网络的基函数如下

模糊神经网络系统的总输出为

式中w=（w₁，w₂，…，w_j）T，表示模糊系统的参数向量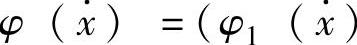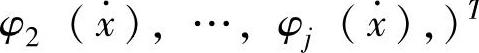；，T，表示模糊基函数向量。

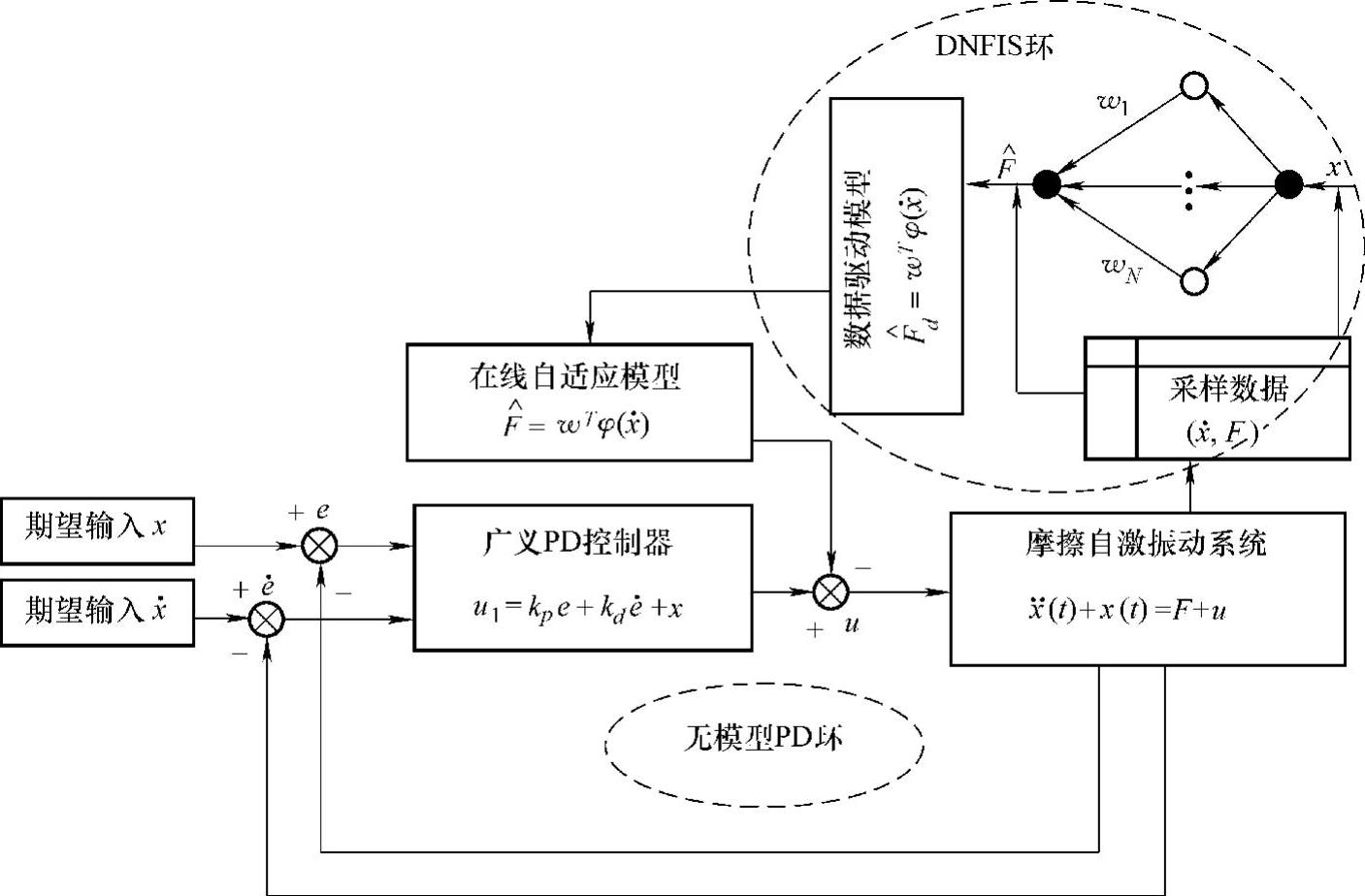
图7-4 基于模糊神经网络补偿的主动控制图