摩擦自激振动的数值分析及控制方法

从摩擦文献可知，到目前为止已提出的摩擦模型有几十种[6]，这些摩擦模型是否都能产生自激振动，以及什么条件下产生极限环振荡一直是人们关心的问题。一种办法是按照上面的思路对这些模型进行某种假设，从而给出解析解。另一种方法是从数值解角度考虑，从而达到控制目的。下面将方程（7-4）中的广义控制力取零（u=0），分析系统在一定时间的响应。参考文献[2]，系统参数取值：m=0.60kg，k=763N/m，F_N=15.0N，v₀=0.3m/s，μ₀=0.25。

Matlab中的四阶五级Felhberg-Runge-Kutta方法为工程技术人员求解非线性微分方程提供了强有力的工具。下面用该方法（ODE45）给出两类摩擦振动问题的数值分析，通过Matlab的ODE45求解，可得到图7-2和图7-3的数值图解。从图可以看出，这两种摩擦力模型都产生了极限环，一个是Coulomb模型

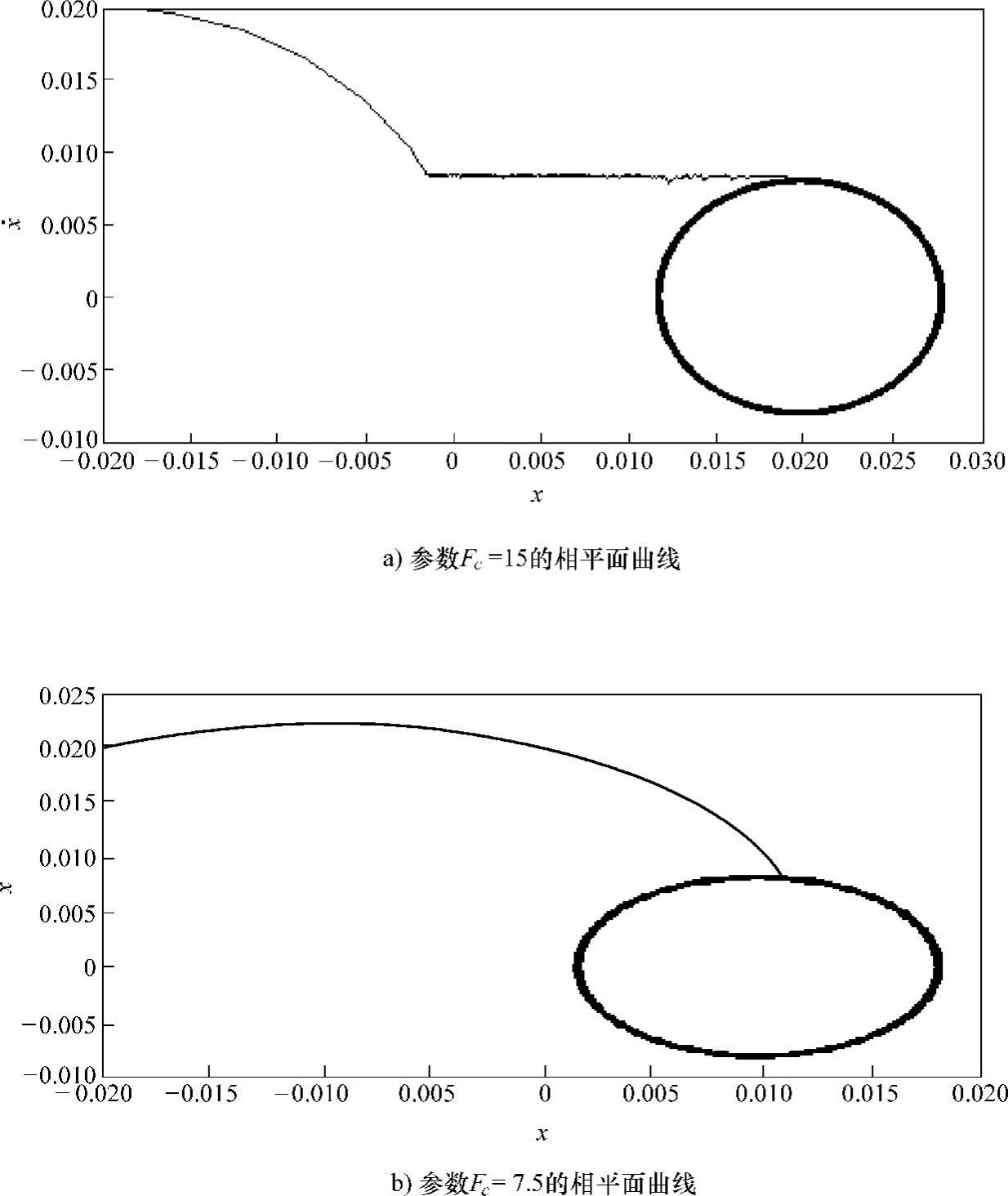
图7-2 Coulomb摩擦诱发的振动极限环

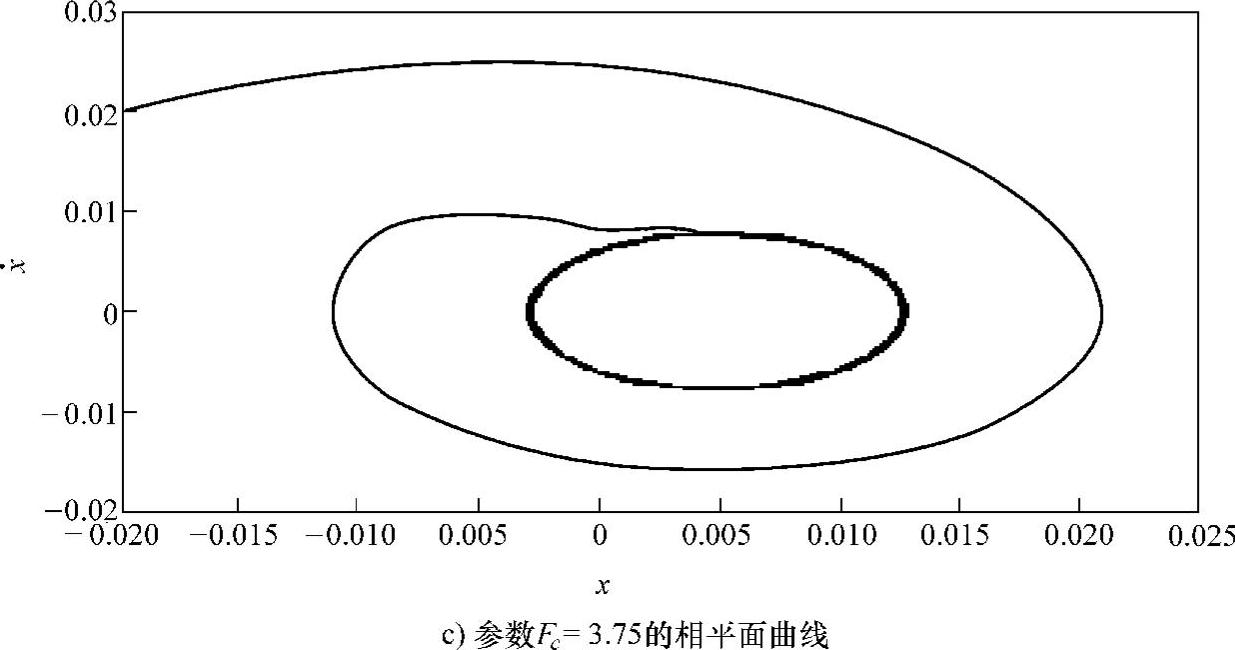
图7-2 Coulomb摩擦诱发的振动极限环（续）

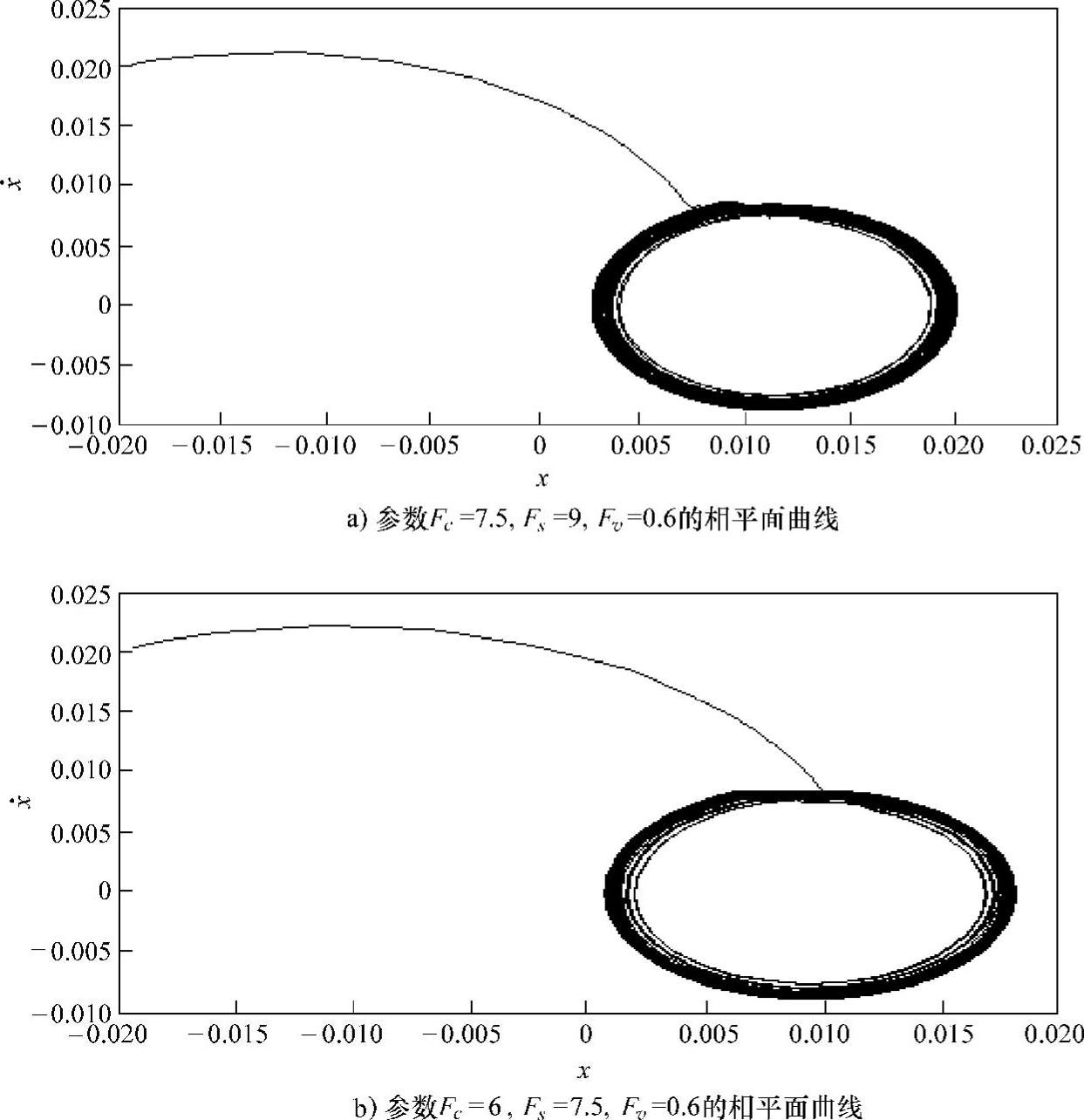
图7-3 Coulomb摩擦诱发的振动极限环

F_f=F_csgn（v） （7-11）

式中F_f——摩擦力；

v——相对滑动速度；(www.xing528.com)

F_c——库仑摩擦力；

sgn（v）——符号函数。

另一个是Stribeck摩擦模型

式中F_s——最小静摩擦力；

F_v——黏性摩擦因数；

v_s——Stribeck速度；

v_s、δs——经验常数。

该模型虽然是静态摩擦模型，但它考虑了Stribeck效应，该模型对摩擦现象描述更为精确。