在这个例子中，我们将验证单参数自适应模糊系统作为摩擦新模型所取得的跟踪控制效果。两种仿真环境和前面叙述的相同。图6-3是在摩擦环境1情况下，也就是真实摩擦力的
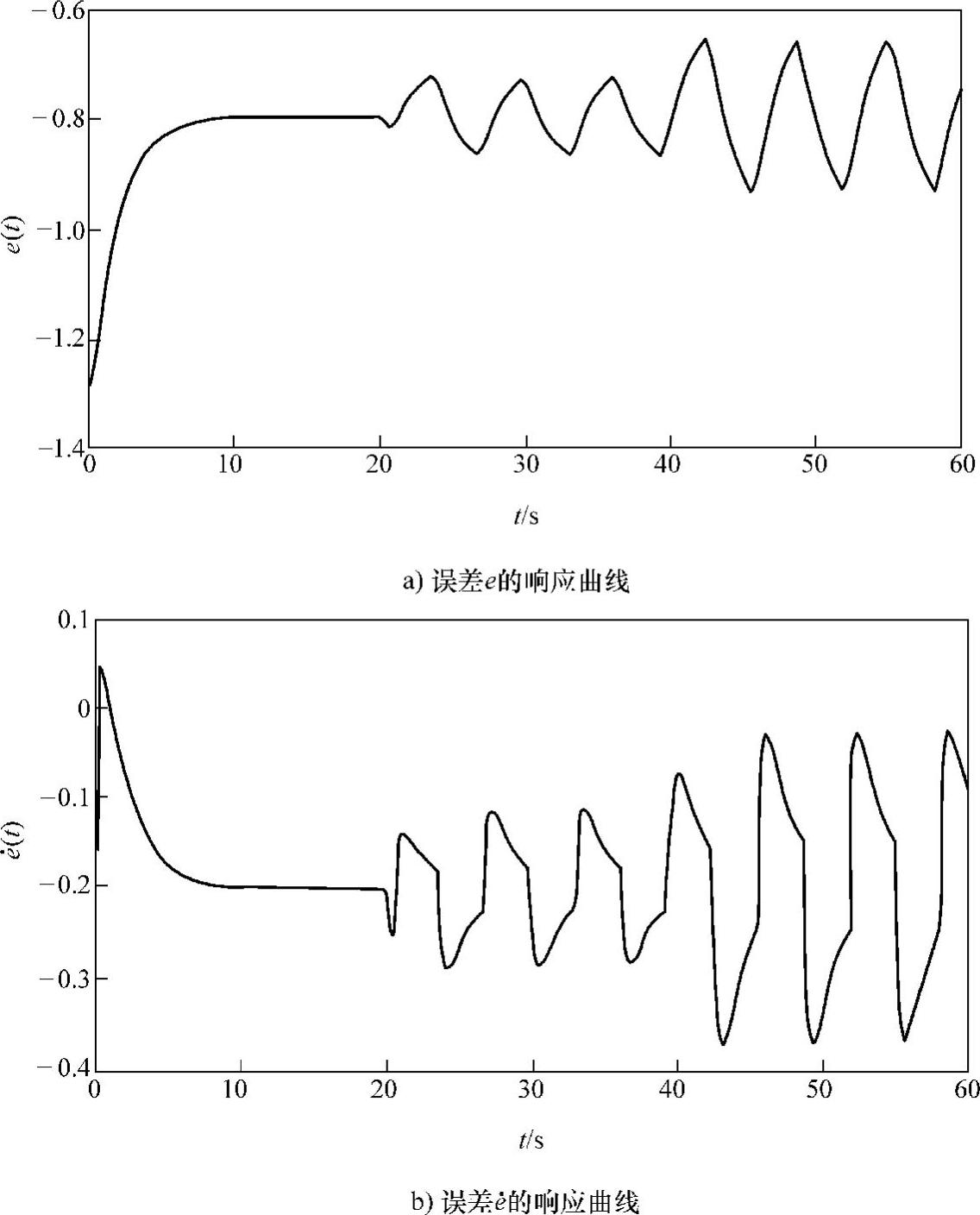
图6-1 系统跟踪误差e的响应曲线（环境1）
图6-2 系统跟踪误差e的响应曲线（环境2）
参数在变化，系统跟踪误差随时间的响应曲线。该结果是控制器u=m（y¨r+k1e·+k2e）+F^f-uc时获得的，其中控制器中的摩擦力F^f采用单参数自适应模糊系统。图6-3是自适应参数仅由跟踪误差e进行调节，而建模误差ε没参与调节形成的。在图6-3的仿真中，控制器的鲁棒补偿控制项的uc的r=0.25，也就是对应着Riccati方程（6-28）的ρ相对较小的情况，也就是干扰信号
对系统的性能干扰较大。
图6-2 系统跟踪误差e的响应曲线（环境2）（续）
图6-3 系统跟踪误差e的响应曲线（环境1）
在图6-3的这个仿真例子中，我们验证了单参数自适应模糊系统作为摩擦新模型所取得的控制效果，其中的控制器的鲁棒补偿控制项uc的r=0.25。在图6-4这个仿真例子中，仍然采用单参数自适应模糊系统作为摩擦新模型，但控制器的鲁棒补偿控制项uc的r=0.08，也就是对应着Riccati方程（6-28）的ρ为较大的情况，也就是干扰信号
较小。从这两个例子可以看出，单参数自适应模糊系统作为摩擦新模型在扰信号
较小的干情况下取得了好的跟踪性能，但在较大干扰信号
时，不是很理想，但比传统摩擦模型要好。(www.xing528.com)
在下面的图6-5和图6-6两个仿真例子里，我们将进一步验证单参数适应模糊系统作自为摩擦新模型，在真实摩擦模型的结构和参数都变化情况下，系统跟踪误随时间的响应曲差线。其控制器设计和自适应参数调整和上面图6-3和图6-4完全相同。图-5和图6-6的例6子进一步说明，即使真实摩擦力的结构发生变化，我们采用的摩擦单参数适应模糊建模技自术和鲁棒控制方案也能保证系统的跟踪性能和稳定性。
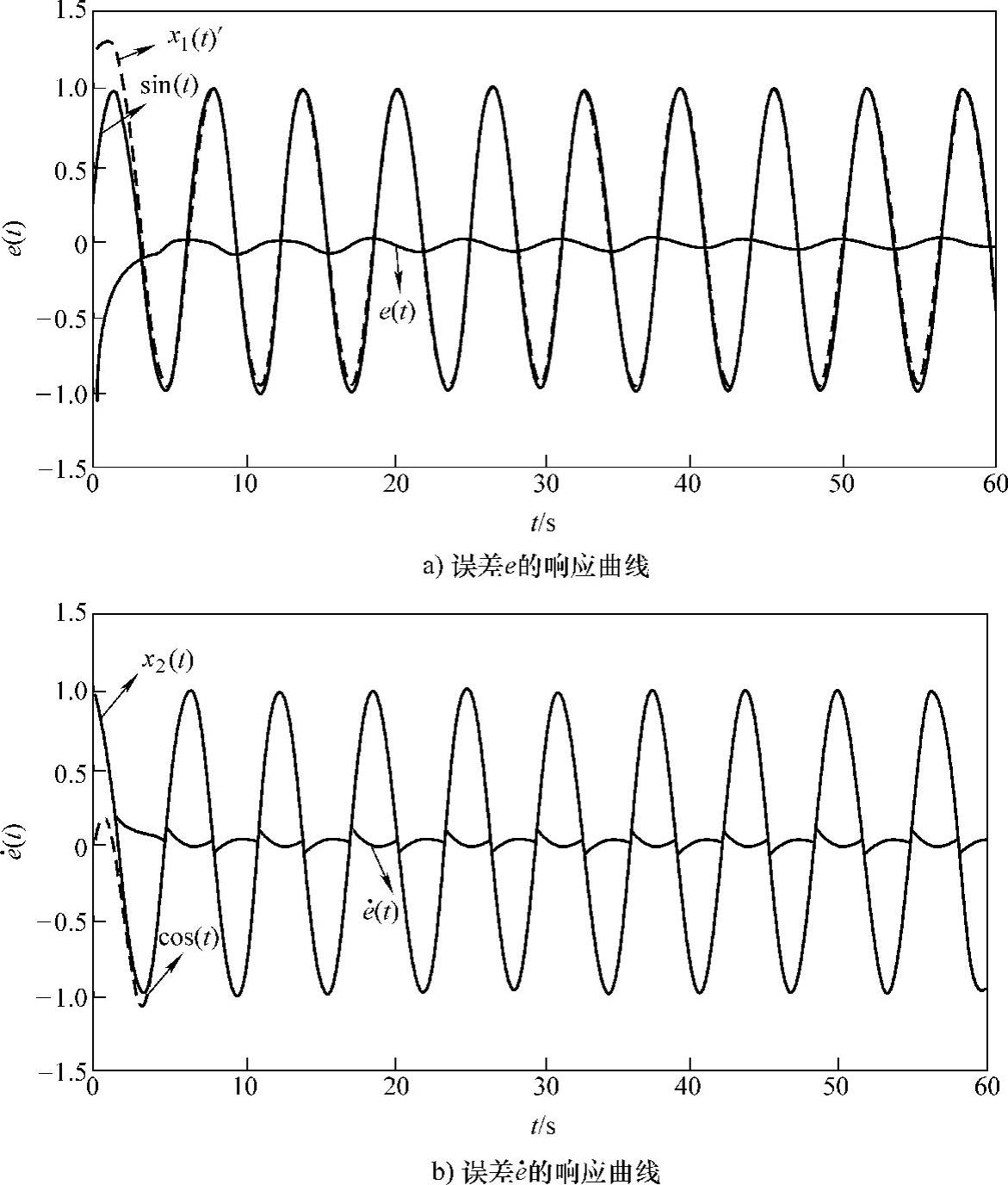
图6-4 系统跟踪误差e的响应曲线（环境1）
图6-5 系统跟踪误差e的响应曲线（环境2）
图6-6 系统跟踪误差e的响应曲线（环境2）
图6-6 系统跟踪误差e的响应曲线（环境2）（续）
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
