由前面的式(6-12)至式(6-15)的分析过程可以看出,如果摩擦估计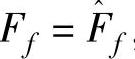 ,则可以获得理想的跟踪效果,但实际中获得理想的逼近
,则可以获得理想的跟踪效果,但实际中获得理想的逼近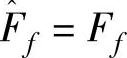 是几乎不可能的。考虑到摩擦建模误差的存在,式(6-6)改取如下反馈控制律
是几乎不可能的。考虑到摩擦建模误差的存在,式(6-6)改取如下反馈控制律
式中uc——考虑摩擦建模误差存在的H∞补偿控制。
把式(6-16)代入式(6-1),经简单整理后可得如下动态误差方程
式中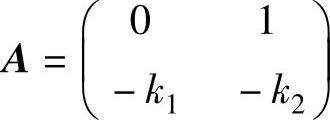 ;
;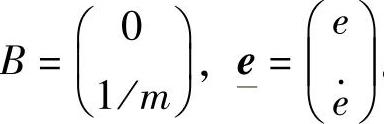 。定义如下最优参数向量为
。定义如下最优参数向量为
定义摩擦建模的最小逼近误差为
那么跟踪误差方程(6-17)能改写成如下形式
联合式(6-15),式(6-20)能被改写如下形式
式中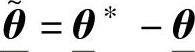 。
。
定义摩擦逼近误差为(https://www.xing528.com)
联合式(6-15)和式(6-19),可以得到如下逼近误差方程
对于反馈控制律(6-16)的关键问题是如何设计自适应模糊系统的参数向量和鲁棒补偿控制项uc,下面将用式(6-23)的摩擦逼近误差ε和跟踪误差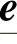 来调节自适应参数向量[6],现将反馈控制律、鲁棒补偿控制项uc以及自适应参数的选取总结如下定理1。
来调节自适应参数向量[6],现将反馈控制律、鲁棒补偿控制项uc以及自适应参数的选取总结如下定理1。
定理1.对于不确定机械系统式(6-1),如果采用控制方案如式(6-24)~式(6-27),其中P为下列Riccati方程(6-28)的正定解,那么系统可获得:①如果 ∈L2[0,∞),获得鲁棒H∞跟踪性能指标;②如果
∈L2[0,∞),获得鲁棒H∞跟踪性能指标;②如果 ∈L∞[0,∞),那么跟踪误差是一致最终有界。
∈L∞[0,∞),那么跟踪误差是一致最终有界。
式中γ和η——指定的常数,投影算子为
在实现上述控制器时,需要注意下面事项:
1)如果自适应方程(6-27)中的η≠0,意味着摩擦建模误差参与自适应参数的调节。
2)在设计实际控制器上时,由于Ff是未知的,为了得到摩擦建模误差ε信号需要高阶信号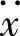 是已知条件。但在仿真时,可以用
是已知条件。但在仿真时,可以用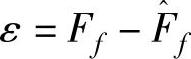 获得建模误差ε信号。
获得建模误差ε信号。
3)实际应用中如果考虑到传感器硬件成本等因素,可以考虑我们提出的模糊观测器法[7]或差分法估计高阶信号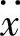 。
。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




