不确定机械问题的建模控制补偿，跟踪误差有界

为了便于问题的描述，考虑下面所用的一维运动系统[1]，系统运动方程如下

式中 m——运动体的质量；

x——运动体的位移；

u——控制力；

F_f——不确定摩擦力。

对于给定的有界参考输入信号y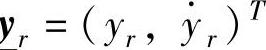假设均有界可测，定义系统输出跟踪误差为e=y_r-y，跟踪误差向量为。

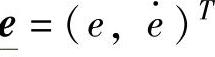目标：设计控制器u=u（e|θ）及自适应参数向量θ的自适应律满足以下所要证明指标：

1）对于给定的减弱水平ρ>0，输出跟踪误差取得如下H∞性能指标

式中 加权矩阵Q=Q^T≥0；

P=P^T≥0；(www.xing528.com)

η>0。

2）如果∈L∞[0，∞），那么跟踪误差是一致最终有界（UUB）。

①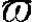表示系统的干扰信号，在这里表示摩擦建模的最小逼近误差。对于∀T∈[0，∞），∈L₂[0，T]空间，也就是满足如下L₂范数定义

对于∀T∈[0，∞），∈L∞[0，∞）空间，也就是满足如下L∞范数定义

②如果系统初始点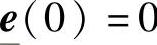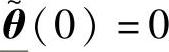，，那么方程（6-2）的H∞性能指标可以写出如下形式

显然，J描述了干扰信号对系统的破坏最严重时的跟踪误差信号与干扰信号的范数比值。J

反映了系统对干扰信号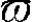的抑制能力，或称为L₂增益。

③如果ρ=∞，表示系统没有干扰信号的干扰，系统获得最小跟踪误差。

④设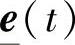是动态系统的跟踪误差，U是Rⁿ中的一个紧集，若对于所有的e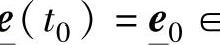U，存在一个δ>0和T（δ，x₀）使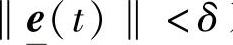对所有的t≥t₀+T都成立，则称跟踪误差是一致最终有界（UUB）。