【摘要】:对于系统,如果系统状态可测且F已知,则理想控制律为把式代入式得E+Kce=0式中,T。获得理想控制器是不可能的。应用式到式经过几步直接的运算后可得如下的跟踪误差方程基于式,上面的方程可以写为定理2.对于系统,如果采用控制方案,系统状态估计用式,自适应参数调节采用式,那么跟踪误差是一致最终有界的。从前文已证和是一致最终有界,并结合上式可知是一致最终有界的,即设计任务达到。
对于系统(5-10),如果系统状态可测且F(x)已知,则理想控制律为
把式(5-44)代入式(5-10)得
E+Kce=0(5-45)
式中,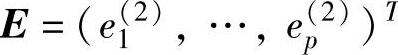 T。
T。
显然如果取Kc=diag[K1,…,KP],且有KI=(ki1,ki2)使系统为稳定的,则有limt→∞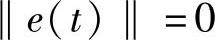 。然而在系统状态不完全可测和F(x)未知情况下。获得理想控制器(5-44)是不可能的。在这种情况下,采用前文所构造的模糊逻辑系统
。然而在系统状态不完全可测和F(x)未知情况下。获得理想控制器(5-44)是不可能的。在这种情况下,采用前文所构造的模糊逻辑系统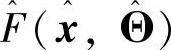 来逼近摩擦力项。取控制律为
来逼近摩擦力项。取控制律为
式中uα——鲁棒补偿控制。
应用式(5-46)到式(5-10)经过几步直接的运算后可得如下的跟踪误差方程
基于式(5-20),上面的方程可以写为
定理2.对于系统(5-10),如果采用控制方案(5-49),系统状态估计用式(5-22),自适应参数调节采用式(5-28),(https://www.xing528.com)
那么跟踪误差是一致最终有界的。
证明:考虑下面基本定义
把式(5-50)代入式(5-47),经简单运算后可得
方程(5-48)的轨迹可表示为
式中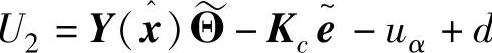 。
。
由范数不等式及文献[5]中的引理2.2可得
式中D1——按指数衰减到零;D2、D3和D4——正数。
从前文已证 和
和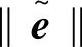 是一致最终有界,并结合上式可知
是一致最终有界,并结合上式可知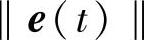 是一致最终有界的,即设计任务达到。
是一致最终有界的,即设计任务达到。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




