有界性分析，状态估计误差一致最终有界

为了应用严格正实理论，输出估计误差（5-24）可以写成下面的形式

式中；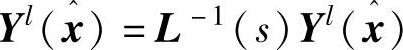

v^l=L^-1v；

dl=L^-1d。

选择一稳定的传递函数L（s），使H（s）L（s）是严格正实的。

根据文献[5]用到的Kalman-Yakub-Popov定理，由于H（s）L（s）是严格正实的，存在一对称正定矩阵P使得

式中Q——对称正定矩阵；

A_c=A-K_oC；

B_c=diag[B_c1，…，B_cp]，且有B_ci=（b_i1，b_i2）T；

C_c=C。

那么，式（5-24）的状态空间实现表示如下

假设1 假设d_i满足条件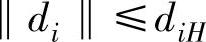，其中，d_iH是正的常数（i=1，…，p）。总的不确定项d_i是由逼近误差和状态估计误差组成，由万能逼近定理可知这种假设是合理的。

定理1 对于系统（5-10）满足上面的假设1，相应的状态估计器为式（5-22），的自适应律为式（5-28），在上式中，v为式（5-29）的鲁棒控制补偿项

式中γ>0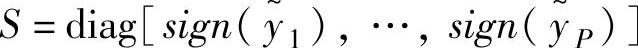；；ρ=（ρ₁，…，ρp）T，且有ρ_i>d_iH；；。

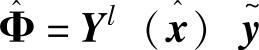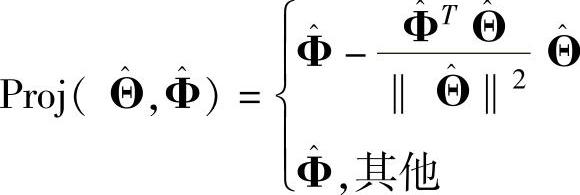如果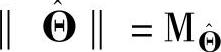且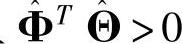，那么状态估计误差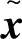是一致最终有界的。(https://www.xing528.com)

证明：取Lyapunov函数为

式中P=P^T>0。

微分式（5-30）可推出

基于式（5-27），可以得到

因为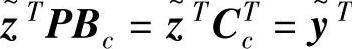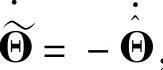，，上式可以写成

因为

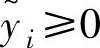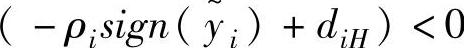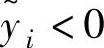对于，由于ρ_i>d_iH，我们可以得到；对于，由于ρi>d_iH，可以得到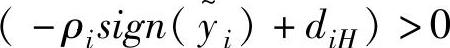，因此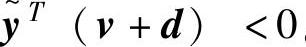。另外，L^-1（s）可取稳定的传递函数和H（s）L（s）是严格正实的，可得到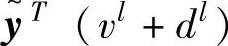。所以方程（5-33）可写成下面不等式

根据自适应律可以得到

按照标准Lyapunov理论，说明状态观测误差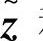和自适应参数误差是一致最终有界的。为了说明状态估计误差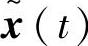的有界性，考虑方程（5-23）的估计误差，轨迹可表示为如下形式

式中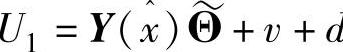d。

由范数不等式及文献[5]中的引理2.2可得

式中C₁——按指数衰减到零；C₂和C₃——正数。

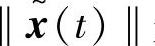因为是一致最终有界并结合上式可知是一致最终有界的，即设计任务达到。