基于非线性系统的模糊观测器与传统高增益观测器的对比仿真研究

非线性系统的状态观测器是指基于非线性系统的输入、输出观测数据估计其不可测的内部状态。非线性状态观测器在科学研究和工程应用领域具有重要价值，如工业过程中的状态反馈控制、航空制导系统、飞行轨迹重构、飞行目标跟踪、环境监控、故障诊断、生化反应的状态提取等。从对象模型已知和未知角度来分，观测器设计方法基本上有两类：已知对象模型[1-3]和未知对象模型[4-6]。已知对象模型是对象模型的结构和参数是完全或部分知道，观测器的构造依赖于对象模型和输入、输出观测数据，如经典的线性Luenberger观测器以及Marino等人提出的非线性广义Luenberger自适应观测器等。未知对象模型方法设计观测器是不需要对象模型是已知的，而只是通过输入、输出观测数据构造观测器，其中比较流行的是高增益观测器。非线性系统的广义Luenberger自适应观测器要求被观测对象模型结构已知的条件，我们知道在实际系统中的对象模型结构很难确定，故非线性系统的广义Luenberger自适应观测器应用到实际中有一定难度。

近年来，用模糊系统研究结构和参数均未知的非线性系统的自适应控制得到了重视，以Lyapunov稳定性理论为基础并结合监督控制、H∞控制和滑模控制等方法得到了广泛的研究与应用[7-13]。上述成果中，自适应模糊控制算法都利用了系统状态是完全可测的条件。而在很多实际系统中的状态变量并不完全可测，如机器人系统中机器人的角位置可以通过编码器精确得到，但对机器人角速度的处理一般很少用硬件测速仪直接检测，因为这种方法增加了成本同时被检测的信号易被噪声污染。对机器人角速度的处理一般采用估计方法：

1）通过检测到的角位置采用数字差分方法求出角速度。

2）设计状态观测器估计角速度。在对机器人位置定位调节及跟踪要求较精确的情况下，采用差分方法所得到的角速度及跟踪效果并不十分理想，近些年采用观测器方法得到了重视[14]。

近几年来，国内外一些学者研究了基于观测器的自适应模糊控制问题，我们知道应用最多的模糊系统是基于T-S模型的模糊系统和基于基函数模型的模糊系统。无论是基于T-S模型的模糊观测器还是基于基函数模型的模糊观测器，它们都不需要被控对象模型的结构和参数已知的条件，而只是通过输入、输出观测数据构造模糊观测器，所以它们本质上都是不依赖被控对象模型的。基于基函数模型构造模糊观测器的自适应输出反馈控制只是在近几年得到了关注，相对来说它还不成熟、问题比较多。

基于基函数模型构造模糊观测器的自适应输出反馈控制在近几年的一些文献中得到了研究，下面简要分析这些文献中存在的问题及需要改进的地方。

在文献[15]中，观测器方程为下面的式（5-1）、控制器方程中的u_s监督补偿控制项及自适应参数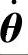中都是用误差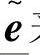来调节的，也就是下列方程

式中；。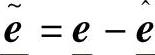

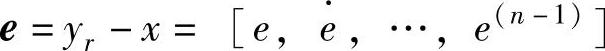可见在控制器又用到了全部状态，而实际上x₁可用（因为y=x₁），而x₂等是不可用的，所以说此控制器还是基于完全状态反馈的，关于该文更详细的评论参见文献[16]。

文献[17]针对单变量系统给出了模糊观测器和自适应控制器，但该文还存在以下几个问题需要改进，该文在应用严格正实得到方程

要求P=P^T>0和B_c=[0…b_m]^T条件，上面方程是无解的。(www.xing528.com)

该文在仿真中只对角位置x₁进行了状态估计和跟踪，而对角速度x₂并没有进行状态估计和跟踪。而实际上应主要是对x₂进行状态估计与跟踪，因为x₁的信息是可测的。该文是针对跟踪误差进行观测，而不是直接对状态进行观测，也就是用如下跟踪误差方程来观测状态

由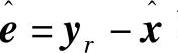可以进一步推导出状态x的观测方程。

文献[15，17]这种做法如果只是研究基于观测器的控制问题是可取的，但在实际中观测器并不是只用到控制问题，也可用到故障诊断等其他问题中。故我们认为文献[15，17]设计的间接模糊观测器并不具有普遍意义。虽然可以用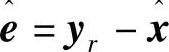可以推导出状态x的观测方程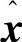，但要求的条件是知道参考输入y_r。

最近，A.Boulkroune教授于2008年在国际杂志《Fuzzy set and systems》发表的论文[18]系统地总结了该方面的主要论文有16篇，其中对14篇论文进行了评论，认为这些论文存在严重错误或不正确等问题。而我们早年在《American Control Conference》发表的文献[19]是仅有的两篇之一没有被评论的，认为是合理的。在此会议论文基础上，我们系统地分析了国内外自适应模糊观测器所存在的问题，我们设计了单输入单输出系统的自适应模糊观测器和输出控制器，该方法具有更好的通用性。这方面的成果发表在国际期刊[20]，我们在该文所设计的模糊观测器和其他论文的主要不同在于：

1）采用类似经典的线性Luenberger观测器，以及Marino等人提出的广义Luenberger自适应非线性观测器的方法，即直接对状态进行观测并给出了观测误差收敛性证明，而不是对跟踪误差进行观测。或者说，我们设计了基于模糊系统的非线性广义Luenberger自适应模糊观测器，是对非线性广义Luenberger自适应观测器的一种扩展。

2）针对前文中的不可实现和无解问题进行了改进，把观测器设计、控制器设计，稳定性分析和系统实现进行了有效的整合。

3）在仿真中对观测误差和跟踪误差都进行了详细的仿真验证。

4）为了验证模糊观测器的有效性，在相同控制器和参数的情况下与常用的传统高增益观测器进行了对比仿真研究。

最近，将我们提出的单输入单输出系统的自适应模糊观测器技术扩展到含摩擦环节的多输入多输出机械系统的摩擦建模与控制补偿中[21]。