不确定机械问题建模与控制方法的对比

把本文所采用的角速度估计方法及PD控制器用于单自由度机械手系统的仿真，该机械手（见图4-1）的动态模型为

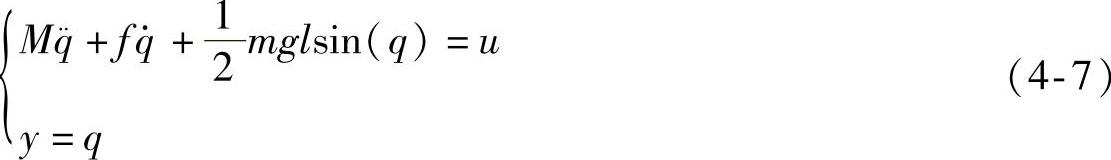
式中，分别为机械手臂的角位置，角速度和角加速度；

l——连杆长度；

g——重力加速度；

m——杆的质量；

f——摩擦系数；

M——运动惯量；

u——驱动力矩。设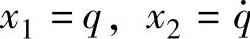，那么上式能被改写成如下状态方程

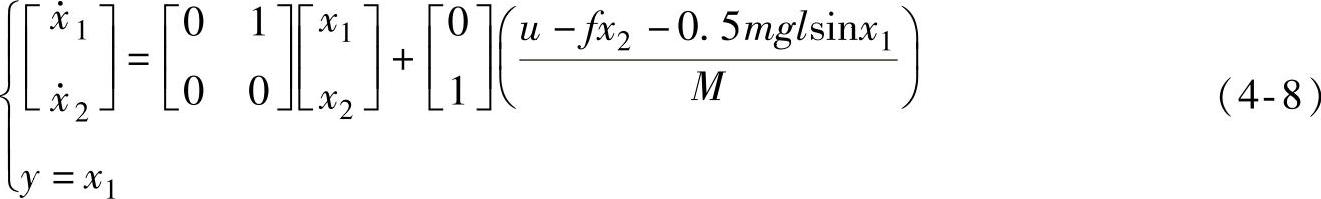
系统参数选择：m=1，l=1，M=2，f=0.6，x（0）=[00]^T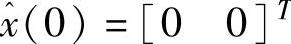，T，x^d₁=1，(www.xing528.com)

x₂^d=0，H_P=0.03，H_P=0.03，H_v=0.06，k_P=160，k_d=10，T=0.001，ε=0.001，控制器的输出限幅为[-10+10]。

用高增益状态观测器式（4-3）和控制器式（4-4）构成了系统的基于高增益状态观测器的输出反馈控制；而差分方法式（4-5）和控制器式（4-6）构成系统了系统的基于差分方法的输出反馈控制。下面将从仿真角度对比这两种输出反馈控制的效果。

从图4-3可以看出，在系统动态调节过程，基于高增益观测器方法形成的定位调节控制问题要好于数字差分方法。也就是用高增益观测器方法形成的定位调节（图4-3a）经过短暂的动态过程达到了期望的位置，而差分方法的动态过程明显要长些。而图4-4是角速度的响应曲线，从该图也可以看出基于高增益观测器方法形成的定位调节控制问题要好于数字差

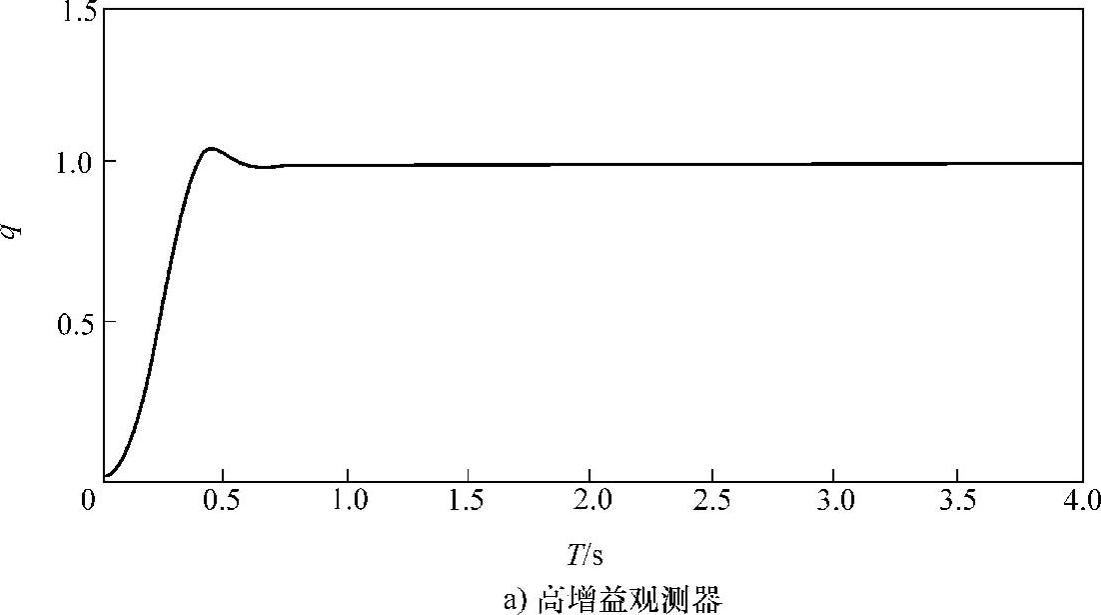
图4-3 基于状态估计的机器人角位置q的输出曲线

分方法。通过上面的仿真，可知基于观测器方法的摩擦补偿模型与输出反馈控制取得了良好的控制效果。

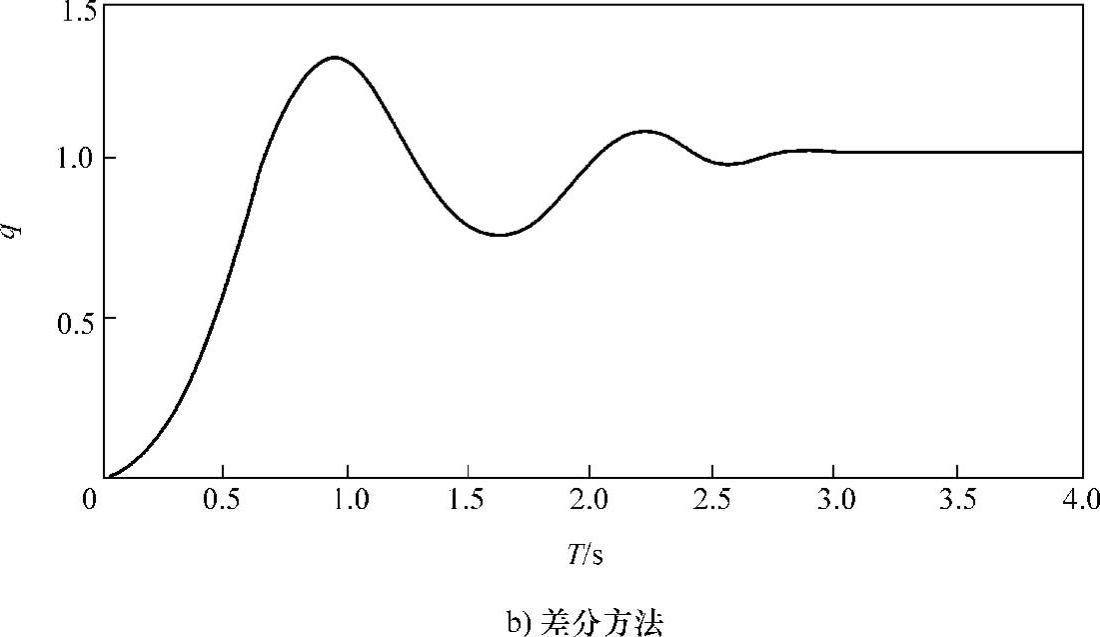
图4-3 基于状态估计的机器人角位置q的输出曲线（续）

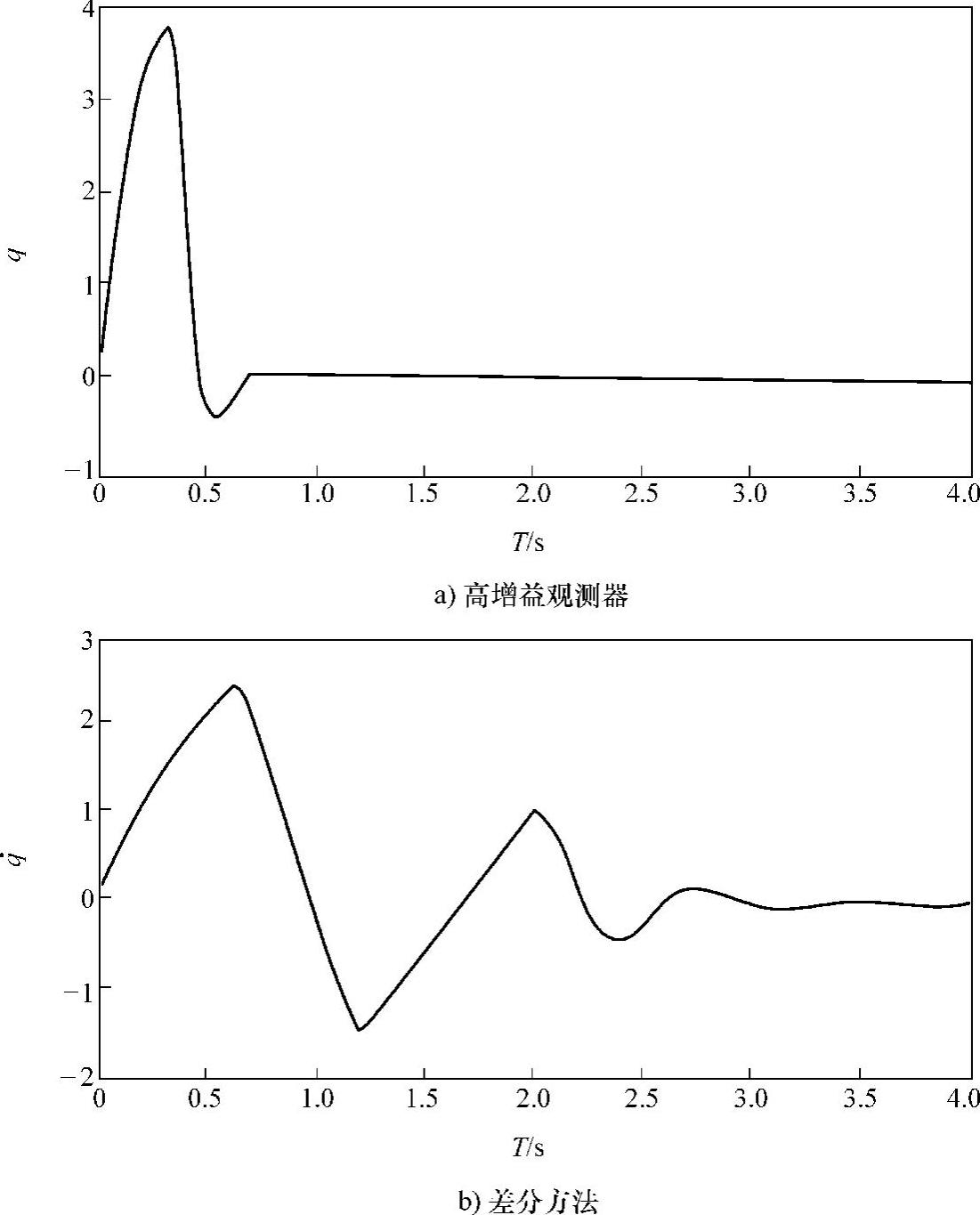
图4-4 基于状态估计的机器人角位置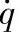的输出曲线