摩擦模糊模型的自适应机制及控制补偿

为了便于问题的描述，考虑文献[2]所用的一维运动系统，系统运动方程如下

式中m——运动体的质量；

x——运动体的输出位移；

F——摩擦力；

u——控制力。

若式（3-10）中的摩擦力已知，可采用基于摩擦模型补偿的PD经典控制器，也就是如下方程

式中e=x_d-x；

x_d——已知的系统期望输出位移；k_p和k_d——分别表示比例和微分系数。

把式（3-11）代入式（3-10）可得如下动态误差方程

上面的控制器在运动系统中得到了广泛应用，它在定位调节控制中取得了十分满意的性能；在跟踪控制中能保证跟踪误差的有界性。

式（3-12）的结果是在假设摩擦力F已知情况下得到的。对摩擦项F来说，由于建立精确摩擦模型的高难性，得到精确控制算法（3-11）是不可能的。为此，拟用前文的模糊系统替代方程（3-11）中的摩擦项，可得如下方程

式中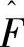——前文提到的模糊系统。把式（3-13）代入式（3-10）可得如下动态误差方程

因x_d是有界的、已知的参考输入，故可以把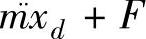看成是摩擦的广义函数，式（3-14）等价如下方程

式中k₂=m^-1k_d；

k₁=m^-1k_p；

F_g=mx¨_d+F。

下面用模糊系统对广义摩擦项进行逼近，定义最优参数向量为

式中Ω_θ——θ的界。(www.xing528.com)

那么最小逼近误差可表示如下方程

由式（3-9）和式（3-17）知，式（3-15）可写成

式中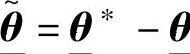。式（3-18）也等价如下形式

式中；；；。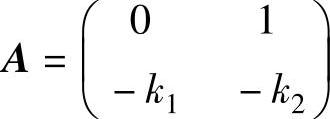

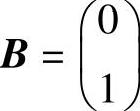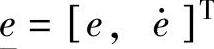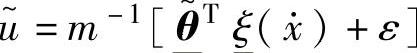定理1：如果采用式（3-20）和式（3-21）的主动控制器，自适应参数由式（3-22）在线调节

式中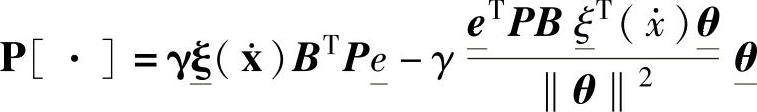，是投影算子。正定解P>0满足下面的李雅普诺夫方程（3-23）A^TP+PA=-Q （3-23）

那么，跟踪误差收敛到某一紧集。

证明：取Lyapunov函数为

求V的微分，可推出

因为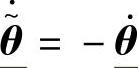，并结合（3-23）可得

由方程（3-22）和（3-23），上面方程对消一部分后可得到

因此，可以得到

式中ε₀——ε的界。

从式（3-28）可以看出其是变号函数，但只要方括号中的项大于零就可得V·<0，即满足下式

由标准Lyapunov理论可知，只要误差项大于式（3-29）的右边项，因V·<0，那么跟踪误差就会减小。这也说明跟踪误差的有界性，即

式（3-30）的有界性说明闭环系统的跟踪误差最终进入某一个紧集。由式（3-30）还可以看出，跟踪误差的界依赖于建模误差的界ε₀，如果建模误差为零，那么将取得零跟踪误差。所以说模糊系统对摩擦的逼近精度对系统的精度提高是至关重要的，故本方案首先基于数据挖掘技术建立了摩擦的静态模型，然后根据Lyapunov稳定性建立了摩擦的动态模型，从而提高对摩擦的逼近精度。