不确定机械问题的建模与控制补偿

下面用一个例子来说明本文提出的DM算法比iWM算法具有更好的鲁棒性。首先分别用iWM算法和DM算法产生各自的模糊规则库，然后用各自的模糊规则库形成相应的模糊系统逼近下列非线性函数

设输入x的范围为[-1，1]，隶属度函数采用高斯函数；输出y的隶属度函数采用三角函数。

在实际工程中，得到全部理想数据是十分困难的。我们得到的数据常常带有一些干扰数据，因此算法具有一定的抗干扰性（鲁棒性）是十分重要的。下面通过一个实验对比两种方法的鲁棒性。设理想样本数据为T={t₁，t₂，…，t₁₁}。为考察鲁棒性，在样本集里增加一个坏的数据记录t₁₂，也就是样本数据为T={t₁，t₂，…，t₁₁，t₁₂}。

表2-4 第三种情况的样本数据（非理想情况）

第一种情况：将输出x和输出y都分割成5个模糊集，分别用{A₁，…，A₅}和{B₁，…，B₅}表示。在坏的数据干扰情况下，用iWM和DM算法计算的平均值和支持度如表2-5a和表2-5b所示，由此表计算的模糊模型如图2-8所示。其中，图2-8a表示用iWM算法获得的模糊模型的逼近仿真结果，曲线误差为：0.21899；图2-8b表示用DM算法获得的模糊模型的逼近仿真结果，曲线误差为：0.13225。图2-8a的逼近精度明显低于图2-8b的逼近精度，这种情况说明DM算法在完备性方面优于iWM算法。

表2-5a 计算平均值（情况一）

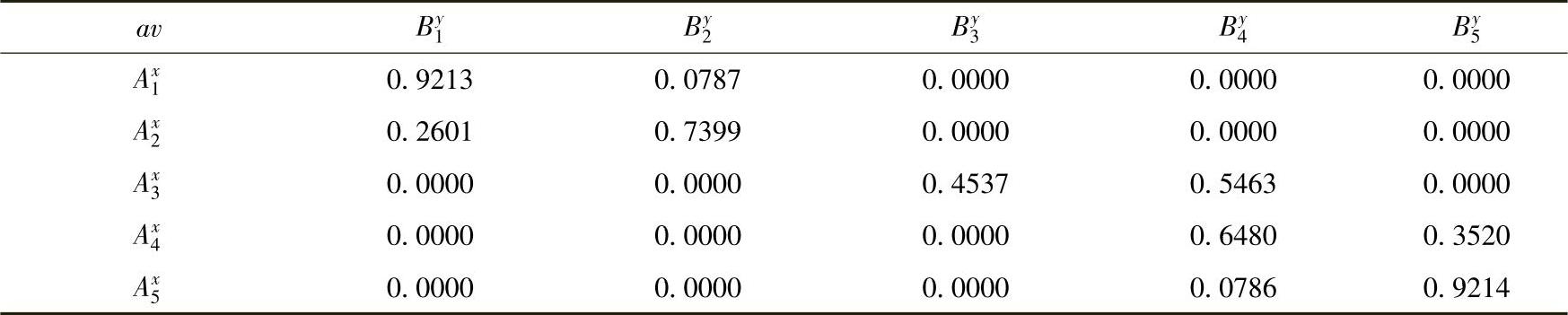
表2-5b 计算支持度（情况一）

(www.xing528.com)

图2-8 估计模型和实际模型

第二种情况：将输出x和输出y都分割成7个模糊集，分别用{A₁，…，A₇}和{B₁，…，B₇}表示。在坏的数据干扰情况下，用iWM和DM算法计算的平均值和支持度如表2-6a和表2-6b所示，由此表计算的模糊模型如图2-9所示。其中，图2-9a表示用iWM算法获得的模糊仿真结果，曲线误差为：0.14296；图2-9b表示用DM算法获得的模糊仿真结果，曲线误差为：0.0797。图2-9a的逼近精度明显低于图2-9b的逼近精度，这种情况说明DM算法在完备性方面优于iWM算法。

表2-6a 计算平均值（情况二）

表2-6b 计算支持度（情况二）

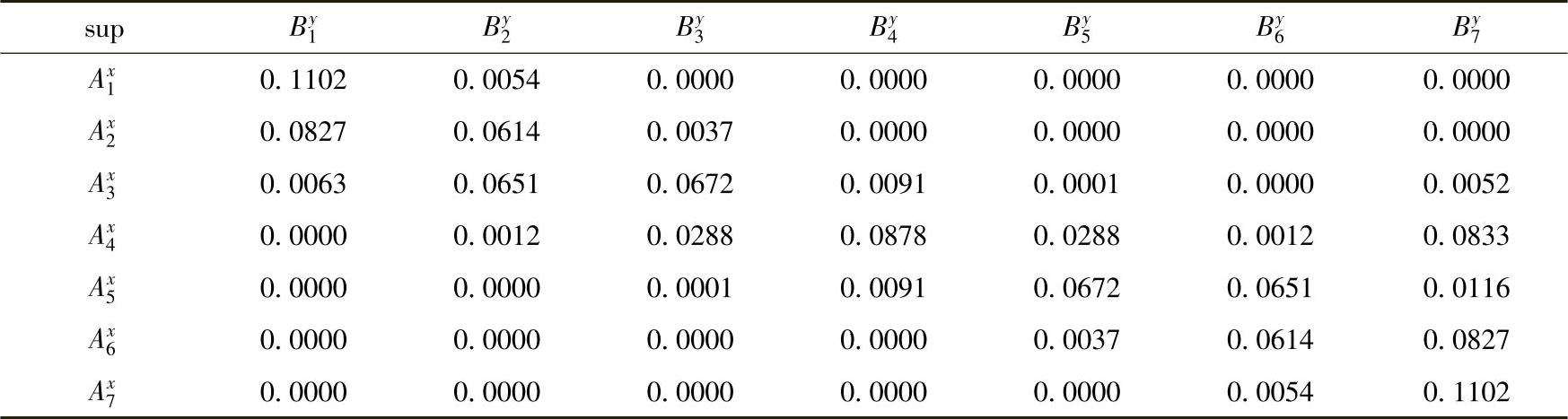
图2-9 估计模型和实际模型