设给定 一组期望的输入-输出数据对
（x1（1），x2（1）；y（1）），（x1（2），x2（2）；y（2）），……… （2-28）
式中x1，x2——输入；
y——输出。
现在的任务是：从式（2-28）给出的输入-输出数据对中产生一组模糊“如果-则”规则，并用这些规则确定出所需要的模糊逻辑系统f：（x1，x2）->y。
这种方法分如下5步组成。
步骤1：把输入空间和输出空间划分为模糊区间
为了方便描述和理解，考虑一个两输入单输出的系统。设x1，x2和y的取值范围分别为[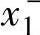
，
]，[
，
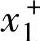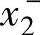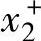]和[y-，y+]，这里，变量的取值范围是指该变量很可能处于该范围以内。将每一个变量的取值范围再划分成2N+1个区间，将这2N+1个区间分别表示为SN，…，S1，CE（中点），B1，…，BN（从小到中到大），且每个区间都对应一个模糊隶属函数。在图2-3的例子中，x1的取值范围分为5个区间（N=2），x2的取值范围分为7个区间（N=3），y的取值范围分为5个区间（N=2）。其隶属函数的形状均是三角形的；区间的中点对应于三角形的纵向顶点，且在该点上隶属函数取值为单位值1。三角形的另两个横向顶点分别位于两个相邻区间的中点上，且隶属函数在这两个顶点上的值等于零。当然，区间的划分和隶属函数的选择也存在其他的选择。
步骤2：由已知的输入-输出数据对产生模糊规则
首先，求出不同区间上已知数据x1（i），x2（i）和y（i）对应的隶属度。例如图2-3中，x1（1）在B1区间上的隶属度为0.8，在B2上为0.2，而在其他区间上为0。同样，x2（2）在CE上的隶属度为1，而在其他区间上均为0。其次，将已知数据x1（i），x2（i）和y（i）分别定位于最大隶属度对应的区间上。例如，在图2-3中，x1（1）被认为在B1区间上，x2（2）被认为在CE区间上。
最后，从每一对较满意的输入-输出数据对中产生一条规则。例如：
（
，
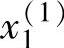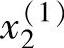；y（1））⇒[
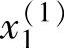（B1上隶属度最大，0.8），
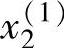（S1上隶属度最大，0.7），y（1）（CE上隶属度最大，0.9）]->规则1：如果x1为B1且x2为S1，则y为CE。（
，
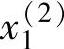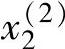；y（2））⇒[x1（2）（B1上隶属度最大，0.6），
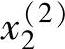（CE上隶属度最大，1），y（2）（B1上隶属度最大，0.7）]->规则2：如果x1为B1且x2为CE，则y为B1。
用上述规则产生的是“逻辑与”规则，即在规则中只有当“如果”部分的条件都同时满足，“则”部分的结果才会发生。就现在的问题而言，即如何从数据信息中得出模糊规则来，只有“逻辑与”型规则满足要求。因为前提条件是某个输入向量的不同分量需要同时满足。
步骤3：为每一条规则赋予一个置信度
由于有许多对数据信息，而每一对产生一条规则，这样就很可能出现自相矛盾的规则，即出现“如果”部分相同而“则”部分不相同的规则。解决这个矛盾的一种方法就是为每一个数据对产生的规则赋予一个置信度，最后在自相矛盾的规则中选用具有最高置信度的那条规则。这样就不仅解决了矛盾，而且也使规则的数目大大减少。
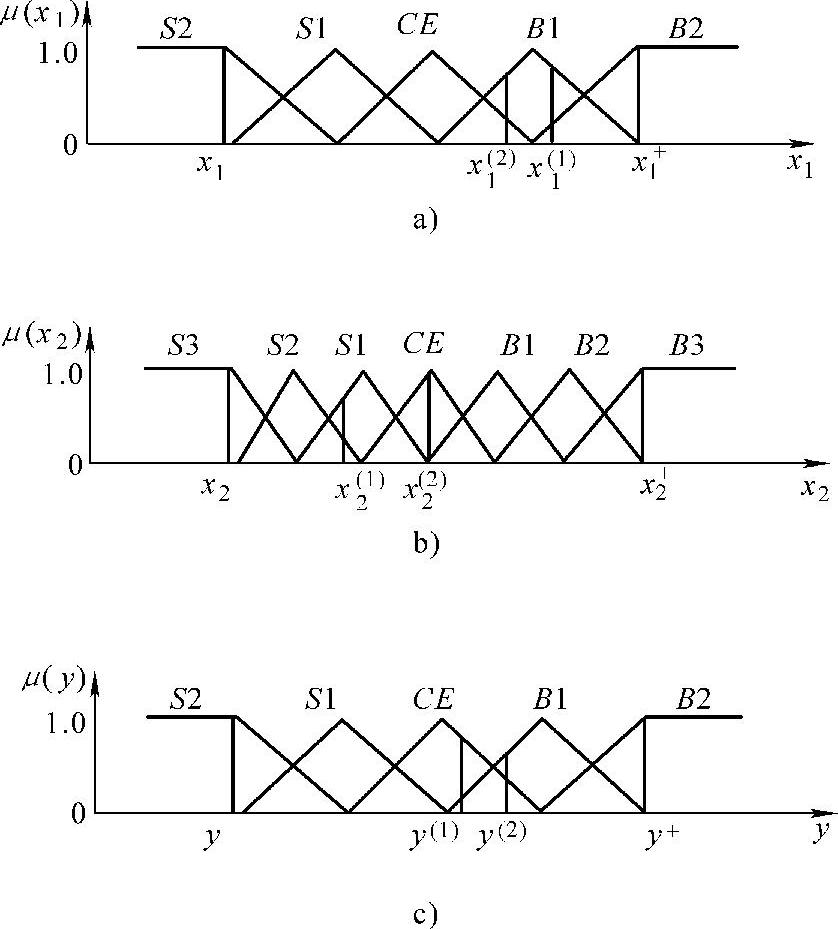
图2-3 变量的隶属度函数
用如下的乘积策略为每一条规则赋予一个置信度：对于“如果x1为A且x2为B，则y为C”这样一条规则，其置信度D（规则）可定义为
D（规则）=μA（x1）μB（x1）μC（y）（2-29）举例说明，规则1的置信度为（见图2-3）
D（规则1）=μB1（x1）μS1（x2）μCE（y）（2-30）
=0.8×0.7×0.9=0.504规则2的置信度为
D（规则2）=μB1（x1）μCE（x2）μB1（y）（2-31）
=0.6×1×0.7=0.42
在实际应用中，常常还会得到这些数据对的某些先验信息。比如，让一个专家来检查所得到的数据对，这个专家就很可能看出哪些数据有用，哪些数据是关键性数据，哪些数据不太合理或由量测误差产生。因此，可以为每一对数据再附加一个信任度以表示专家对该数据可靠性的相信程度。(www.xing528.com)
设数据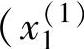
，
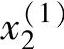；y（1））的附加信任度为μ（1），则再将规则1的置信度重新定义为
D（规则1）=μB1（x1）μS1（x2）μCE（y）μ（1）（2-32）即一条规则的置信度定义为规则各分量的隶属度与产生该规则的数据信任度之乘积。这一点在实际应用中非常重要，因为在真实数据中，每个数据的可靠性不同，例如，某些数据可能非常不合理（既“反常数据”）。对合理的数据给一个较高的信任度，而对不合理的数据设一个很低的信任度。这样，就把专家对数据的认可程度作为另一种信息，用同一种形式包含进去了。如果强调数据的客观性而不想加进专家对数据信息的主观认同，则只需将所有数据的专家信任度全部取单位值就可以了。
步骤4：组合模糊规则库的产生
图2-4给出的查寻表格就是一个模糊规则库，用以下的准则把模糊规则填入表中的空格：组合模糊规则库中的规则即可以来源于数据产生的规则，也可来源于语言性规则，如果模糊规则库中某一空格对应的规则不止一个，则选用具有最大置信度的那一条规则。这样，数据和语言两类信息就用一种统一的方式一组合模糊规则库统一起来了。如果语言规则为“逻辑或”（即规则中“如果”部分的任一条件满足，就有“则”部分发生），则它填满“如果”部分所对应区间的某一行或某一列所有的空格。例如有这样一条语言规则：“如果x1为S1或x2，为CE，则y为B2”，则对图2-4所表示的模糊规则库来讲，就需将B2填满Sl列的七个空格和CE行的五个空格。所有这些空格中B2的置信度都等于这条“逻辑或”规则的置信度。，
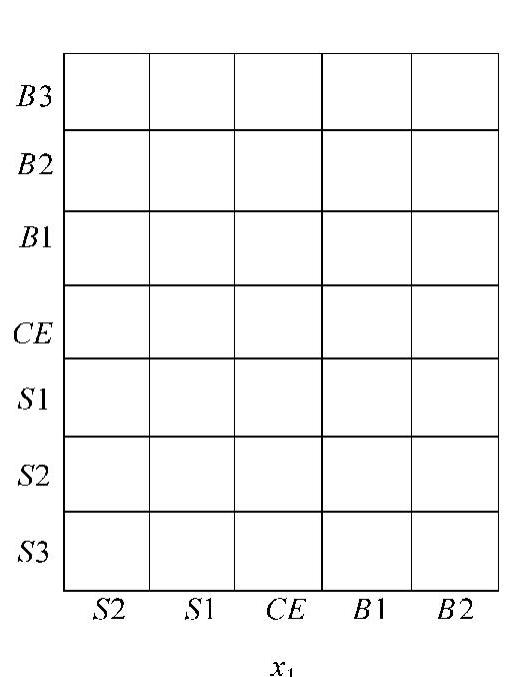
图2-4 WM方法的查寻表格
步骤5：根据组合模糊规则确定出映射关系
用下面的模糊消除策略来从已知的输入（xl，x2）中求出输出控制量y:首先，对于已知的输入（xl，x2），需用乘积运算来综合第i条规则的所有前提条件，以求出（xl，x2）相对应的输入控制的置信度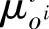
，即
式中 Oi——规则i的输出区间：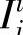
——规则i中第j个分量输入区间。
对规则1有
则用下列的中心平均模糊消除公式就可以求出输出y
式中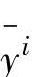
——区间Oi上中心点的取值（模糊区间中心点的定义是：在该区间上隶属函数取
得单位值1的所有点巾，（横轴）绝对值最小的点为中心点）；
M——组合模糊规则库中模糊规则的数目。
从步骤1到步骤5可以看到，这个方法的整个过程既简单又直接，因为它是一个一步生成过程，不需要费时的反复学习：因此，这个方法同样具有模糊系统优于神经网络的一大优点，即构造起来简单又迅速。
上述五步过程可以很容易地推广到一般性多输入一多输出的情况。步骤1到步骤4均与输入和输出个数无关。在步骤5中，只需将方程(2-33)中的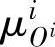
代之以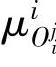
即可，这里j表示输入向量的第，个分量（D；为规则：的第，个分量所对应的区间；胁对所有的j都取相同的值），同时将方程(2-35)变换为下式
式中
的中心点。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
