不确定机械问题的建模与控制补偿实战

19世纪末德国数学家George Contor创立的集合论已经成为现代数学的基础，每个数学分支都可以看作研究某类对象的集合，因此集合的理论统一了许多似乎没有联系的概念。

定义1（集合）：集合一般是指具有某种属性的、确定的、彼此间可以区别的事物的全体。将组成集合的事物称为集合的元素。通常用大写字母A，B，C等表示集合，而用小写字母a，b，c表示集合内的元素。元素和集合之间的关系是属于或不属于的关系，当元素a属于集合A时，用a∈A表示；反之用a∉A来表示。

经典集合中元素与集合的关系可以通过特征函数表示法来刻画，如某一集合A的特征函数定义如下

从中可以看出，一个元素和集合的关系只有两种，即或者是属于A，或者是不属于A。

用上述经典集合的定义所表达的概念内涵和外延都是明确的，但在人们的思维和语言表达中，有许多没有明确外延的概念，即模糊概念，如“高个子”、“青年”等。模糊概念无法用经典集合加以描述。为解决这一问题，Zadeh提出了模糊集合（Fuzzy Sets）的定义。

定义2（模糊集合）：论域U上的一个模糊集合A是指对于论域U中的任一元素u∈U，都指定了[0，1]闭区间的一个数μ_A（u）∈[0，1]与之对应，它叫做u对A的隶属度。这意味着定义了一个映射μ_A

这个映射称为模糊集合A的隶属函数。

模糊集合的表达方式有以下几种。

1.U为有限集

当U为有限集{u₁，u₂，…，u_n}时，通常有以下3种方式

（1）Zadeh表示法

在上式中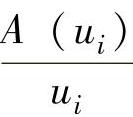，并不表示分数，而是表示论域中的元素u_i与其隶属度A（u_i）之间的对应关系；“+”也不表示求和，而是表示模糊集合在论域U的整体。

例2.1在由整数1，2，…，5组成的论域中，既U={1，2，3，4，5}，讨论“非常小”这一模糊概念。根据经验，可以定量地给出他们的隶属函数，模糊集合“非常小”可表示为

上式表明：“1”的隶属度为1，说明“1”为“非常小”的可能性最大；“5”的隶属度最小，说明“5”为“非常小”的可能性也最小。(www.xing528.com)

（2）向量表示法

A=（A（u₁），A（u₂），…，A（u_n））（2-10）采用向量表示法，上述例子2.1中的A可表示为

A=（1，0.64，0.36，0.16，0.04）（2-11）在向量表示法中，隶属度为0的项不能省略。有时也将上述2种方法结合起来表示为

则上述例子2.1可表示为。向量表示法对于模糊集合的运算十分方便。

（3）序偶表示法

将论域中的元素u_i与其隶属度A（u_i）构成序偶来表示A，则

A={（u₁，A（u₁）），（u₂，A（u₂）），…，（u_n，A（u_n））}（2-13）采用序偶表示法，例子2.1中的A可表示为

A={（1，1），（2，0.64），（3，0.35），（4，0.16），（5，0.04）}（2-14）此种方法隶属度为0的项可不写入。

2.U为有限连续域

当U为有限连续域时，Zadeh给出如下记法

μ同样，并不表示“分数”，而表示论域上的元素u与其隶属度A（u）之间的对应关系；∫既不表示积分也不表示求和记号，而是表示论域U上的元素u与其隶属度A（u）对应关系的一个总括。

例2.2以年龄作论域，取U=[1，100]，Zadeh给出的“年老”Q与“年轻”Y两个模糊集合的隶属函数为

采用Zadeh表示法，“年老”Q与“年轻”Y两个模糊集合可写为