不确定机械问题的摩擦动态模型

伴随着对摩擦行为的认识，人们开发了摩擦的动态模型。动态摩擦模型是不仅仅把摩擦力描述为相对速度的函数，还包括其他时变参数，如摩擦力是速度和位移的函数。

1.Dahl摩擦模型

著名的Dahl摩擦模型[15-16]是为了更好地描述带有摩擦力矩的控制系统发展起来的，是对动态摩擦特性的最简单描述。通过引入一个内部中间状态变量z，Dahl模型定义的微分方程形式为

式中x——位移；

σ₀——刚度系数；

α——拟合参数，通常情况下取为1。

这个模型也可以用下面时域形式来描述

当α=1时，Dahl模型成为

若令

F_f=σ₀z （1-18）

则式（1-18）变为

当时间t趋于∞时，由式（1-18）和式（1-19）给出的稳态摩擦力为

F_f=σ₀z=F_csgn（v） （1-20）此时，Dahl摩擦模型退化为库仑摩擦模型。

Dahl模型是最简单的动态摩擦模型，理论上容易理解，是建立其他动态模型的重要基础。该模型是连续模型，利用切向柔顺行概念将预滑动位移引入摩擦模型，避免了静态模型中状态切换的不连续问题。Dahl模型描述了静摩擦下接触峰的弹簧行为，并且开创性地引入了平均变形的概念，即用状态变量z来描述无数个接触峰的平均变形。该模型的数学特性在文献[17]中已被研究，包括解的存在性和唯一性，以及迟滞作用等。虽然Dahl模型描述了预滑动位移，也可以预测摩擦滞后，但是它既没有描述静摩擦力，也没有捕捉到Stri-beck效应[18]。

2.Bliman-Sorine模型

Bliman和Sorine受Dahl模型的启发，试图将Stribeck摩擦加入该模型，在Rabinowicz试验[19]的基础上提出了Bliman-Sorine模型[20-21]。该模型是一个2阶Dahl模型，可以看成两个1阶Dahl模型的关联。假设摩擦力依赖于速度符号sgn（v）和空间变量s

Bliman-Sorine模型还可以通过微分方程来表示

式中v_s=sgn（v）。

1阶摩擦模型为

式（1-22）可写为

当F₁=F_c，F₁/ε_f=σ₀，α=1时，其形式与Dahl模型是一致的。

1阶模型式（1-22）未能描述静摩擦，因此需引入2阶模型

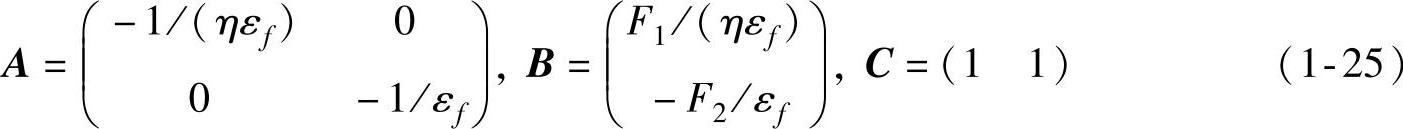
式中_η、ε_f、F₁和F₂——模型相关参数。

Bliman-Sorine证明了1阶和2阶模型都是耗散系统[21]，当ε_f趋向于零时，1阶模型近似于经典的库仑摩擦模型，而2阶模型近似于静摩擦+库仑摩擦模型。Bliman-Sorine模型只能给出运动时瞬时速度的Stribeck效应，而当速度和摩擦力处于稳态关系时，则无法描述Stribeck效应，而且该模型不能描述摩擦记忆和可变静摩擦力等现象，因此限制了其应用。

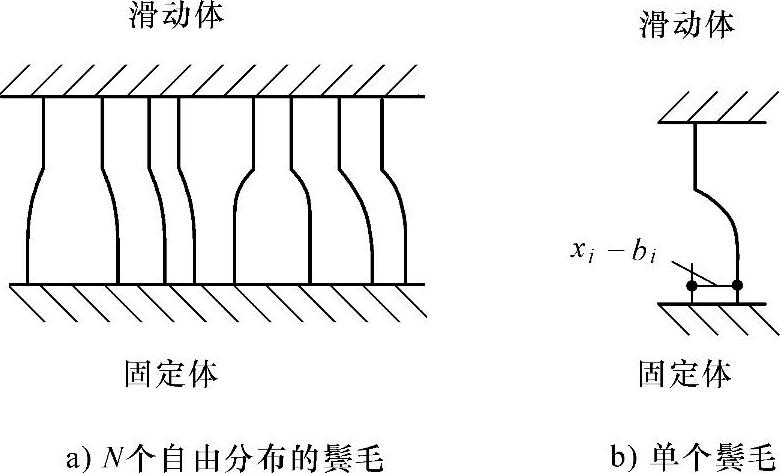
图1-4 鬃毛模型示意图

3.鬃毛模型

为了从微观角度来描述两个接触表面间接触点的随机行为，Haessing和Friedland提出了鬃毛模型[22]，将接触表面看成是大量的弹性鬃毛的接触。鬃毛模型的简化原理如图1-4所示

当接触面产生相对运动时，滑动体上的易弯鬃毛相对于固体上的刚性鬃毛之间将像弹簧一样相互作用从而产生摩擦力，该摩擦力定义为

式中N——鬃毛的总数；

σ₀——易弯鬃毛的刚度；

x_i——易弯鬃毛的相对位置；

b_i——刚性鬃毛位置。

界面间的摩擦力是每一对结合的鬃毛间产生的力的总和。当易弯鬃毛的挠曲超过Δ时，结合点会断开，而在瞬间新的结合点的随机位置又会形成，这个位置定义为

b_i+1=bi+uniform（Δ）sgn（x_i-b_i） （1-27）函数uniform是随机分布的鬃毛的位置，分布距离范围为0～Δ。

随着鬃毛数量N的增加，模型的复杂性将增加，当采用20～25根鬃毛时，得到的效果较好。鬃毛模型的优点是较为准确地捕捉了微观摩擦的随机特性，但是它没有考虑到计算耗时的问题。由于鬃毛间的空间非常细小以及鬃毛突然断开的不连续性，使得该模型在仿真中的积分算法需要极短的时间步长，计算耗时量非常大，因而在数值计算上该模型的效果不是很好，一般不用于仿真。

4.复位积分模型

在文献[22]中，Haessing和Friedland还提出了复位积分模型，该模型是为了减少鬃毛模型的计算量而设计的，同时它保留了鬃毛模型描述微观黏滑摩擦现象的能力。该模型中引入了一个附加状态变量z来描述鬃毛结合部位的应变

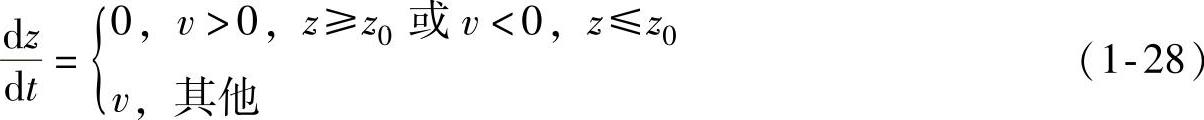
摩擦力表示为

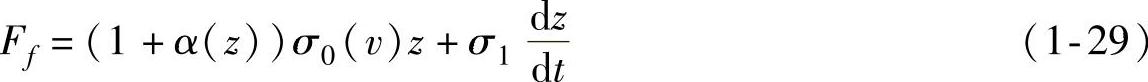
式中σ₀（v）——刚度，速度的函数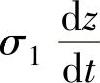；——阻尼项，其只有在黏滞情况下才有效。

静态摩擦力根据函数α（z）来获得

(www.xing528.com)

如果|z|<z₀，该模型描述的黏滞阶段摩擦，摩擦力是z的函数。当鬃毛变形达到它的最大值z₀时，变量z保持为常数，摩擦力值下降，因为α（z）=0。在滑动状态下摩擦力为速度的任意函数，由σ₀（v）项决定。当复位积分器的弹簧应变率和阻尼系数达到无穷大时，复位积分模型可以接近Karnopp摩擦模型。该模型在仿真方面比鬃毛模型有效，但是变量z是不连续的，而且还涉及|z|<z₀的检测问题。

5.LuGre摩擦模型

在瑞典兰德工程技术学院和法国格勒诺布尔实验室的共同努力下，法国学者Canudas de Wit在Dahl摩擦模型的基础上提出了LuGre模型[23]。该模型是Dahl模型的扩展，同时采纳了鬃毛模型的思想，即在微观下接触表面可以看成是大量的具有随机行为的弹性鬃毛。不同的是，鬃毛模型描述的是摩擦的随机行为，而LuGre模型是基于鬃毛的平均变形来建模。

鬃毛的平均变形用状态变量z来表示，建模为

摩擦力由鬃毛的挠曲产生，可以描述为

F_f=σ₀z+σ₁z·+σ₂v （1-32）

式中σ₀——鬃毛的刚度；

σ₁——微观阻尼系数；

σ₂——黏性摩擦系数。

函数g（v）描述了Stribeck效应，方程形式为

式（1-32）中阻尼系数σ₁一般为常数，称为LuGre模型的标准参数化形式。当g（v）=F_c，σ₁=σ₂=0时，LuGre模型可以简化成Dahl模型。

若假设鬃毛的平均变形处于稳态运动，即z·=0，并且忽略黏性摩擦项σ₂v，则稳态情况下的摩擦力就成为Stribeck摩擦，转变成下面形式

F_f=σ₀z=g（v）sgn（v） （1-34）

LuGre模型中共有6个参数，其中σ₀和σ₁是动态参数，F_c、F_sv_s和σ₂是静态参数。静态参数的辨识相对比较简单，而动态参数的辨识由于引入不可测量的状态变量z比较复杂。该模型用一个1阶微分方程描述了诸多摩擦现象，包括库仑摩擦、黏性摩擦、预滑动、可变静摩擦力、Stribeck摩擦和摩擦滞后等，较其他模型更能体现真实摩擦现象。文献[24]从数学角度讨论了LuGre模型具有耗散性的充分和必要条件。

和离散的Armstrong七参数摩擦模型相比，LuGre模型属于连续模型，不同摩擦状态之间能够平滑地过渡，更容易实施。Bliman-Sorine模型和LuGre模型是Dahl模型的两个不同扩展形式，二者之间的详细关系见文献[25，26]。

LuGre模型也可以考虑为摩擦系数，如文献[27]中对回转关节处的摩擦建立了如下模型

M_f=rF_Nμ（z，z·，v）（1-35）

式中r——摩擦力作用半径；

F_N——正压力。

摩擦系数_μ的形式就是LuGre模型

μ=σ₀z+σ₁z·+σ₂v （1-36）

LuGre模型在具体应用时，也可做适当改动，如文献[28]针对两连杆平面机械臂，在原始LuGre摩擦模型的基础上，对两个关节建立了变化的LuGre摩擦模型

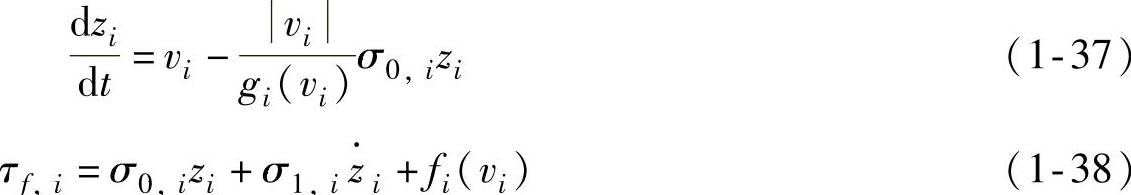
为了更好地拟合该文中的数据，公式中函数g_i（v_i）和f_i（v_i）均采用了不同于原始LuGre摩擦模型的形式

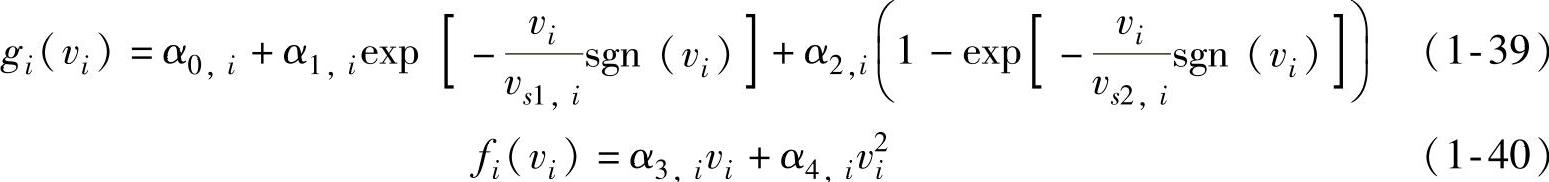
式中v_s1，i、vs2，i——模型参数。

6.Leuven摩擦模型

尽管LuGre摩擦模型是个比较完善且容易实施的摩擦模型，但仍有学者指出了不足之处。Swevers[29]指出LuGre模型的缺点主要表现在对迟滞现象描述不充分：没有解释试验中观测到的非局部记忆效应，不能调整任意的“位移-力”过渡曲线，而且在预滑动阶段过于耗散。

因此，Swevers基于LuGre模型提出了一种更加精细的Leuven摩擦模型。该模型采用状态变量z来描述鬃毛的平均变形，由两个方程组成：非线性状态方程和摩擦力方程，其形式为

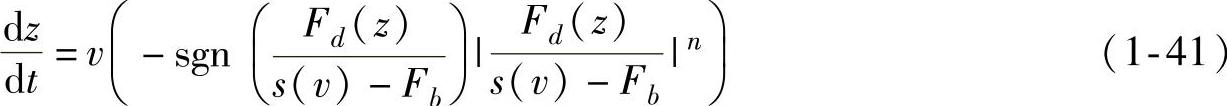
F_f=Fh（z）+σ₁z·+σ₂v （1-42）式中n——描述过渡曲线的系数；

s（v）——描述常速下的摩擦行为，其表达式为

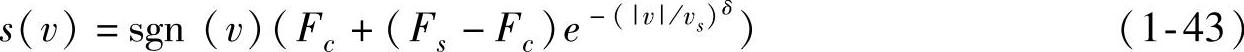
式中F_h（z）——迟滞力，是具有非局部记忆的静态非线性力，由两部分组成

F_h（z）=F_b+F_d（z）（1-44）式中F_b——在速度反向时过渡曲线的起始位置；

F_d（z）——^一定时间内产生的过渡曲线。

Leuven模型不仅包含了LuGre模型所能描述的摩擦特性，还采用了具有非局部记忆的迟滞函数对预滑动区间建立了更为精确的模型。二者的主要区别点在于LuGre模型是用一个线性函数σ₀z来描述迟滞摩擦力，而Leuven模型则用了一个迟滞函数F_h（z）。虽然Leuven模型更加准确，但是它比较复杂，需要6个参数和3项机制（即速度反向、内环闭合和迟滞模型复位）来描述摩擦行为，因此辨识参数的难度大于LuGre模型。

7.广义Maxwell摩擦模型

文献[32]在Maxwell摩擦模型[30-31]的基础上提出了广义Maxwell模型，采用无质量的块弹簧取代了原模型中的弹簧。这些块弹簧在静摩擦阶段表现为弹簧，在滑动阶段会展示摩擦的滑动特性，如Stribeck效应。广义Maxwell模型的主要思想是：采用一定数目并联的弹塑性弹簧来模拟两个表面间微观接触的凸起，每一个弹簧都有自己固有的迟滞特性，

以第i个块弹簧单元为研究对象，在稳态滑动阶段，其状态方程为

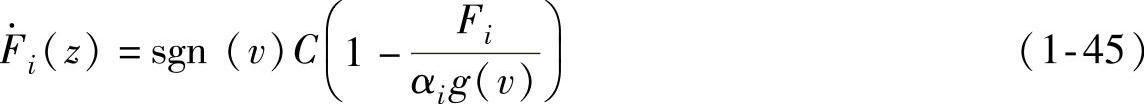
式中C，α_i——常数；

g（v）——描述Stribeck摩擦。

该单元在速度不为零时会一直处于滑动状态。在黏滞阶段，其状态方程为

F·_i（z）=k_iv （1-46）

式中k_i——刚度，是每一个单元都有的独立的参数。

当F_i（z）>α_ig（v）时，这个单元就会开始滑动。通过把所有单元的状态模型加起来再加上黏性摩擦项，就得到了总体摩擦力的表达式

广义Maxwell摩擦模型能够精确描述预滑动区域、滑动区域，也能够捕捉最大静摩擦力、黏滑现象和摩擦滞后等。它与LuGre模型和Leuven模型的状态方程主要不同之处，就是状态方程（1-45）没有将速度v作为一个单独算子。

上述介绍了几种较为重要的动态摩擦模型，还有许多其他模型，如弹塑性摩擦模型、单状态弹塑性摩擦模型、Valanis摩擦模型、通用摩擦模型、时间滞后模型以及单状态和多状态积分摩擦模型等，关于这些模型的详细信息请参阅相关文献。总的来看，动态摩擦模型比静态摩擦模型具有更好的连续特性，能更好描述摩擦的非线性行为。但是，对摩擦行为描述的越全面，其参数辨识难度越大。Dahl模型由于其结构的简单性，已经被用于自适应摩擦补偿研究。LuGre模型是一个比较完善的摩擦模型，能够准确的预测摩擦的各种重要特性，由于其对摩擦环节动态补偿效果较好，因此，该模型以成为工程应用和控制领域研究的一个热点。其他动态摩擦模型由于其自身参数辨识以及计算耗时等方面的局限性，致使它们在实际工程中的应用较少。