解决机械问题的静态摩擦模型

早期人们根据观测和试验，对摩擦的机理进行了数学描述，建立了摩擦的静态模型。摩擦静态模型是将摩擦力描述为相对速度的函数。

1.库仑模型

16世纪早期，达·芬奇在试验观察的基础上，得出了“摩擦力正比于法向载荷，与运行方向相反且不依赖于接触面积”的结论，后来库仑（Coulomb）在达·芬奇研究基础上，将其发展成了库仑模型，摩擦力可表示为下式的形式，如图1-3a所示。

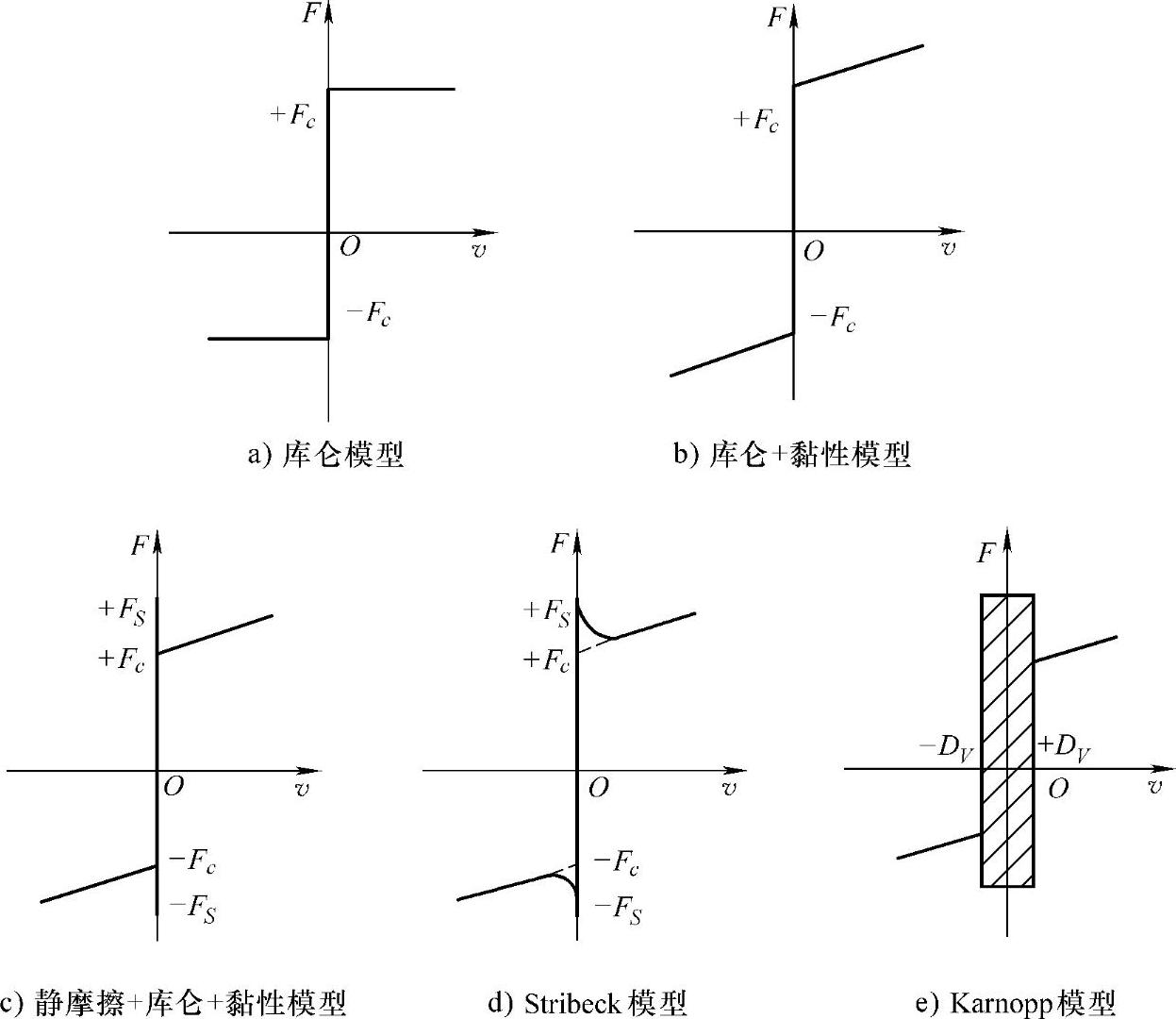
图1-3 几类摩擦模型的示意图

F_f（v）=F_csgn（v） （1-1）

式中F_f——摩擦力；

v——相对滑动速度；

F_c——库仑摩擦力，F_c=μ|F_n|；

μ——摩擦系数；

F_n——法向力；

sgn（v）——符号函数。

这是最早的关于摩擦的定义和模型，摩擦力只是速度的函数。库仑摩擦模型局限于非零速下的摩擦，不能够描述速度为零时的摩擦力情况。在速度为零时，摩擦力可以为零或者介于F_c与-F_c之间的任何值。而且该模型涉及符号函数，使得系统的动力学方程变成了分段函数，从而引入非线性使求解变得非常复杂。

2.库仑+黏性模型

19世纪，随着流体力学的发展，人们发现液体存在黏性，从而导致了线性黏性摩擦模型的出现，描述为

F_f（v）=F_vv （1-2）

式中F_v——黏性摩擦系数；

v——相对滑动速度。

在某些情况下，为了更好地与试验数据相拟合，也可以建立一种与相对滑动速度成非线性关系的黏性摩擦模型，摩擦力可表示为下式的形式

式中δ_v——取值依赖于应用表面的几何形状。

线性黏性摩擦模型通常与库仑摩擦模型组合使用，进而发展成为另一种简单的库仑+黏性摩擦模型，摩擦力可表示为下式的形式，如图1-3b所示。

F_f（v）=F_vv+F_csgn（v） （1-4）

3.静摩擦+库仑+黏性模型

Morin于1833年又引入了静摩擦力的概念，也就是静止时静摩擦力与外力相互作用的思想。试验发现使系统从零速到达一个稳态速度的力要比保持这个稳态速度所需的力大，即静摩擦力水平要高于库仑摩擦力。所以，静态摩擦力F_static与外力F_e有关，有如下函数关系

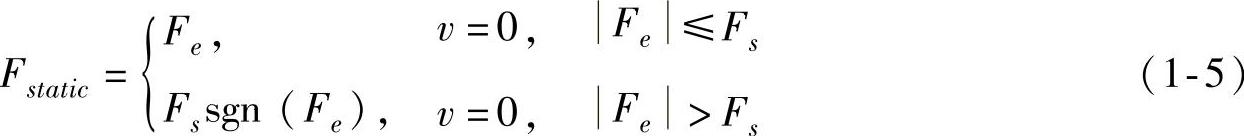
式中F_s——最大静摩擦力。

当v=0时，摩擦力是外力的函数而不是速度的函数，所以采用传统方式以速度为输入、力为输出来描述摩擦力并不是完全正确的。

随着静摩擦概念的引入，形成了至今还广泛使用的经典传统（静摩擦+库仑+黏性）摩擦模型，摩擦力可表示为下式的形式，如图1-3c所示。

F_f（v）=F_static+F_vv+F_csgn（v） （1-6）

4.Stribeck摩擦模型

在上面介绍的摩擦模型均可称为经典摩擦模型，模型中滑动摩擦力都是速度的线性函数，并且静摩擦和动摩擦之间的转换是离散的。但是，Stribeck在1902年试验观察到：摩擦力并不像图1-3c描述的那样，当克服摩擦力后不连续地下降，而是在低速下随着速度的增加而减小，呈现为速度的连续函数。这一现象也称为负斜率摩擦现象。Bo和Pavelescu在1982年提出了一个指数模型来描述Stribeck现象[7]，表达式如下

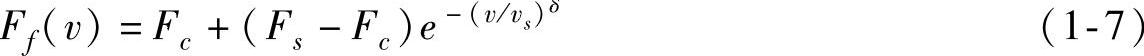(www.xing528.com)

式中v_s——Stribeck速度；

v_s和δ——经验常数。

该模型后经Armstrong完善，添加了黏性摩擦项，最后的表达式如下

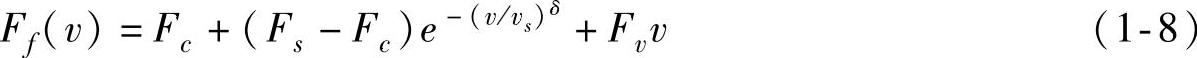
不同学者对δ的取值有不同看法，Bo和Pavelescu将δ的取值范围定为0.5～1之间，而其他学者常取δ=1或δ=2，当δ=1时就得到Tustin模型[8]，当δ=2时就得到Gauss指数模型[9]。Gauss指数模型与Lorentzian模型[10]近似等效，Lorentzian模型的形式如下

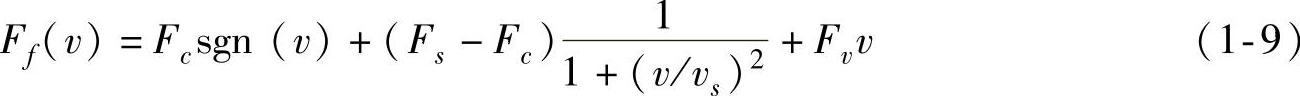
将式（1-5）和式（1-8）综合起来，可以形成一种比经典摩擦模型更为一般的摩擦模型[3]，表达式如下

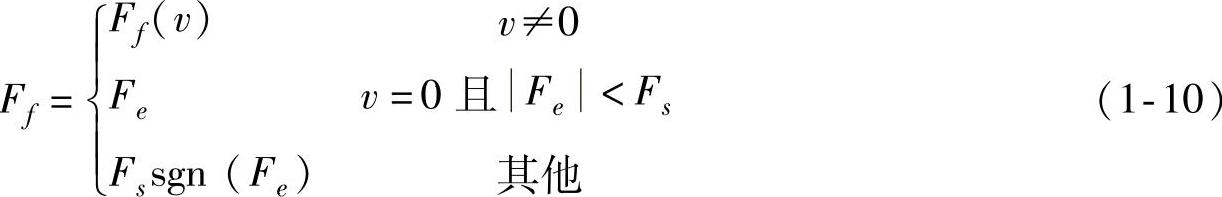
式中F_f（v）——由式（1-8）给出。

该模型很好地描述了低速下的摩擦力行为。用一个衰减指数项体现了负斜率摩擦现象。试验已表明指数模型能以90%的精度近似拟合该区域的真实摩擦力。图1-3d绘制的曲线称为Stribeck曲线。该曲线体现了摩擦力与稳态速度之间的对应关系，也体现了摩擦力的静态特性。该模型表达出了在非常低的速度下，由于Stribeck效应的存在，摩擦力产生不稳定效应。基于该模型可以研究由摩擦引起的黏滑运动和极限环等现象。

5.Karnopp摩擦模型

由于前述几个摩擦模型都需要根据相对滑动速度而进行几个方程之间的切换来描述摩擦力，因此在仿真或控制中需要判断切换点及检查零速，这是比较困难的。Karnopp在文献[11]提出Karnopp摩擦模型，弥补了该项不足。Karnopp摩擦模型定义了一个零速区间|v|≤D_V，如图1-3e。D_V是零附近非常小的速度值，根据不同的工作条件而确定。在±D_V区域外，摩擦是速度的函数，而在±D_V区域之内，速度则被强迫认为是零，此时的摩擦力由系统所受的其他外力决定，其大小等于外力的大小，但要小于最大静摩擦力，方向与外力相反，表达式如下

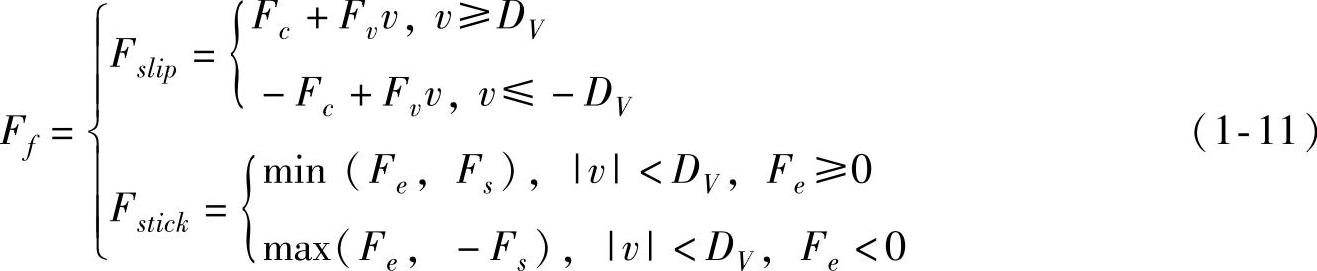
该模型的优点是避免了零速度检测问题以及黏滞和滑动摩擦状态方程间切换问题[12]，但是D_V的确定还没有明确方法，虽然文献[13]在Karnopp摩擦模型参数的辨识中，通过图解法估计了D_V值，但该方法受噪声影响较大，难以实现。该模型的另一个局限性是零速区间的概念和真实摩擦力不相符。该模型目前一般只用于稳态下摩擦力的描述，不考虑速度变化的情况。

6.七参数摩擦模型

为了捕捉摩擦的预滑动位移，可变的静摩擦力以及黏滑等行为，Armstrong和Dupont提出了七参数摩擦模型[3]。该模型采用3个独立的方程分别描述不同阶段的摩擦，七参数摩擦模型如下：

（1）黏滞阶段（预滑动位移）

F_f（x）=-K_tx（ 1-12）

（2）滑动阶段（库仑+黏性+有记忆效应的Stribeck摩擦）

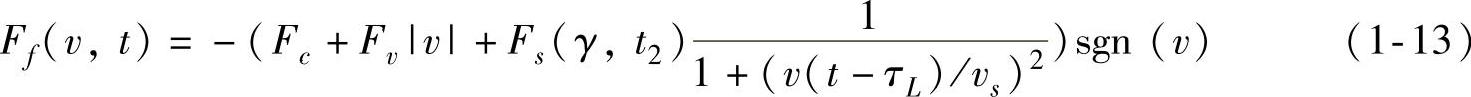
其中可变的静摩擦力为

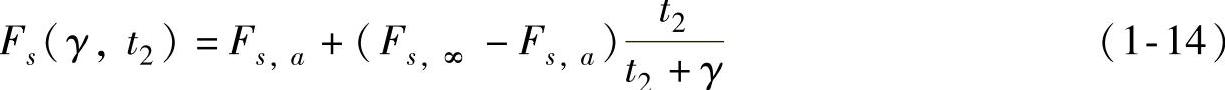
式中F_s——Stribeck摩擦的幅值；

F_s，a——^Stribeck摩擦前一个滑动阶段末端的幅值；

F_s，∞——Stribeck摩擦停止阶段的幅值；

K_t——静态接触时的切向刚度；

v_s——Stribeck速度；

τ_L——摩擦记忆的时间常数；

γ——可变静摩擦参数；

t₂——零速区的停滞时间。

该模型是一个离散的动态摩擦模型，7个参数分别为F_c、F_v、F_s，∞、K_t、v_s、τ_L、γ。

1992年，Plycarpou和Soom报道了其在精确的动态摩擦测量试验中观测到的各种摩擦现象[14]，七参数摩擦模型均能够定性地预测出这些摩擦现象，包括预滑动、库仑摩擦、黏性摩擦、Stribeck效应、摩擦记忆以及可变静摩擦力等。尽管如此，由于该模型包含7个参数，参数辨识非常困难，目前还没有一套成型的参数辨识方法。模型中涉及两个状态空间的切换问题，从物理学角度，这样的切换是不合理的。因此，七参数摩擦模型实际应用受到很大限制。