概率统计应用中的相关与回归分析基本原理

变量的相关关系，按照两者变动的方向可以分为正相关和负相关两类.正相关是指相关系数为正，即两个因素同方向变动，一个增大另一个也增大，反之亦然.而负相关是指相关系数为负，即两个因素按反方向变动，一个增大另一个反而减小，反之亦然.相关分析是回归分析及进一步统计解释的基础.

回归分析是研究一个或者多个变量的变动对另一个变量的影响程度的方法，根据已知的资料或数据，找出它们之间的关系表达式，用自变量的已知值去推测因变量的值或范围，它实际上是研究因果关系.

回归分析就是研究变量之间相关关系的一种数理统计分析方法.在回归分析中，主要研究以下几个问题：

（1）拟合：建立变量之间有效的经验函数关系.

（2）变量选择：在一批变量中确定哪些变量对因变量有显著影响，哪些没有实质影响.

（3）估计与检验：估计回归模型中的未知参数，并且对模型提出的各种假设进行推断.

（4）预测：给定某个自变量，预测因变量的值或范围.

当回归分析主要研究变量之间的线性相关关系时，称为线性回归分析，否则称为非线性回归分析.

回归分析按照影响因变量的自变量的多少，又可以分为一元回归分析和多元回归分析.

线性回归过程中包括一元线性回归和多元线性回归.线性回归过程可以给出回归方程的回归系数估计值（回归系数参数估计和区间估计）、协方差矩阵、复相关系数R、因变量的最佳预测值、方差分析表等，还可以输出变量值的散点图等.

线性回归过程对数据的要求是：自变量和因变量必须是数值型变量.对于因变量的所有观测值（样本）应该认为是来自相互独立的等方差的正态总体，并且因变量与各自变量之间应具有一定的线性关系.

1.一元线性回归

一元线性回归是在排除其他影响因素或假定其他影响因素确定的情况下，分析某一个变量（自变量）是如何影响另一个变量（因变量）的最为常用的统计方法.在一元线性回归模型下，通常假设变量间的关系是线性的，但是这种线性关系并不是确定的，而是附加了随机扰动，是一种不完全确定的相关关系.

模型：y=β0+β1x+ε，ε～N（0，σ2）.

即y的取值由两部分组成：来自x的线性影响部分β0+β1 x及随机误差ε的影响，这里β0，β1为待定系数，随机误差ε则表示除x对y的影响以外其他因素对y的影响.

对一组观测值（xi，yi）（i=1，2，…，n），满足yi=β0+β1 xi+εi，其中εi相互独立，且εi～N（0，σ2）（i=1，2，…，n）.

找一条最好的直线通过n个已知的观测点，实际上就是寻找满足如下关系式的直线参数β0，β1，使得.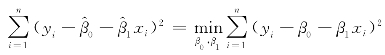

利用高等数学方法可求得：

另一个问题就是σ2的无偏估计，可证明的无偏估计为

2.多元线性回归

一般来说，如果因变量的变化原因可以由一个主要变量加以说明，其他变量的影响可以忽略，则可以用一元回归模型来分析；相反，如果其他变量对因变量的影响不能忽略，就要用多元回归模型来分析.在多元回归模型中，最重要也最常用的是多元线性回归模型.

模型：y=β0+β1 x1+β2 x2+…+βmxm+ε，ε～N（0，σ2），其中β0，β1，β2，…，βm为未知参数.

设（xi1，xi2，…，xim，yi）（i=1，2，…，n）是（x1，x2，…，xm，y）的n个观测值，则满足

yi=β0+β1 xi1+β2 xi2+…+βmxim+εi(i=1,2,…,n)(www.xing528.com)

3.回归模型的假设检验

当完成回归模型中参数及回归偏差σ2的估计后，还需要对模型进行评价.包括检验采用线性回归是否合适、每一个变量是否对因变量起作用、采用线性回归好坏程度的度量.

（1）回归方程的显著性检验.

H0：β1，β2，…，βm=0，H1：至少有一βj≠0 （j=1，2，…，m）

当原假设H0成立时，说明回归方程不显著，采用线性回归不合适.

当备择假设H1成立时，说明回归方程显著，采用线性回归有意义.

回归方程的显著性检验一般使用F检验，给定显著性水平α，可查表得Fa（m，n-m-1），计算F统计量的数值f.

若f≥Fα（m，n-m-1），则拒绝H0，即认为各系数不全为零，线性回归显著；否则接受H0，认为线性回归不显著.

（2）回归系数的显著性检验.

H0:βj=0,H1:βj≠0 (j=1,2,…,m)

当原假设H0成立时，说明自变量xj对y不起作用，在回归模型中可以去掉.

当备选假设H1成立时，说明自变量xj对y起作用，在回归模型中不能去掉.

回归系数的显著性检验一般采用T检验，给定的显著水平α，查表得ta/2（n-m-1），计算统计量tj的数值.

若|tj|≥tα/2（n-m-1），则拒绝H0，即认为βj显著不为零.

若|tj|<tα/2（n-m-1），则接受H0，即认为βj等于零.

（3）复相关系数.

对一个回归方程来说，即使回归显著，但还涉及回归好坏的度量.对两个随机变量之间，衡量它们的相关程度可以采用相关系数来度量，但对一个因变量和一组自变量两者之间的线性相关程度，则要采用下面介绍的复相关系数来度量.

定义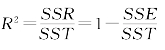

称为回归平方和；

称为残差平方和；

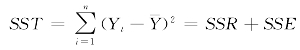称为总离差平方和.

0≤R2≤1，R2的大小直接反映了回归方程的显著程度.R2越接近1，自变量对Y的线性影响就越大，拟合效果就越好.

但复相关系数也有缺点，当采用的自变量越多时，其残差平方和总会减少，从而导致R2增大，而有些自变量的引入可能是多余的.为了更准确地反映参数个数的影响，采用调整的复相关系数（Adjust R2）.R2和Adjust R2越接近1，表示因变量y与各自变量xi的线性相关程度越强.