概率统计应用：正态总体均值差检验

1.已知时，关于μ1，μ2的假设检验

现检验假设

H0:μ1=μ2, H1:μ1≠μ2

在H0成立的条件下，检验统计量

给定显著性水平α，令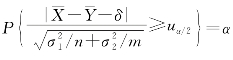，可得拒绝域为

W={|μ|≥μα/2}

例1 某苗圃采用两种育苗方案作育苗试验，已知苗高服从正态分布.在两组育苗试验中，苗高的标准差分别为σ1=18，σ2=20.现都取60株苗作为样本，测得样本均值分别为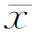=59.34 cm和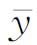=49.16 cm.取显著性水平为α=0.05，试判断这两种育苗方案对育苗的高度有无显著性影响.

解 建立假设

H0:μ1=μ2, H1:μ1≠μ2

由题中给出的数据，我们算出统计量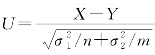的观测值为

另，α=0.05，μα/2μ0.025=1.96，因|u|=2.93>1.96，故拒绝H0：μ1=μ2，认为这两种育苗方案对育苗的高度有显著性影响.

2.未知但时，关于μ1，μ2的假设检验

现检验假设

H0:μ1-μ2=δ, H1:μ1-μ2≠δ

在H0成立的条件下，检验统计量(www.xing528.com)

其中，.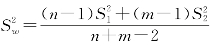

给定显著性水平α，使得

P{|T|≥tα/2(n+m-2)}=α

得到拒绝域为

W={|t|≥tα/2(n+m-2)}

例2 在针织品漂白工艺中，要考虑温度对针织品断裂强力的影响，为比较70℃和80℃的影响有无显著性差异.在这两个温度下，分别重复做了8次试验，得到断裂强力的数据如下：（单位：牛顿）

70℃:20.5 18.8 19.8 20.9 21.5 21.0 21.2 19.5

80℃:17.7 20.3 20.0 18.8 19.0 20.1 20.2 19.1

由长期生产的数据可知，针织品断裂强力服从正态分布，且方差不变，问：这两种温度的断裂强力有无显著差异（显著性水平α=0.05）？

解 设X，Y分别表示70℃和80℃的断裂强力，因此X～N（μ1，σ2），Y～N（μ2，α2），建立假设

H0:μ1=μ2, H1:μ1≠μ2

取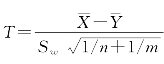为检验统计量，n=m=8，由题中给出的数据可以计算：

检验统计量的观测值为，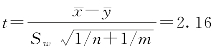

又tα/2（n+m-2）=t0.025（14）=2.145 0，因2.16>2.145 0，故拒绝原假设，即认为这两种温度的断裂强力有显著差异.