【课前导读】点估计给了参数一个明确的数量概念,只是参数的一个近似值,且并没有反映出这个近似值的误差范围,而区间估计正好弥补了点估计的这一缺点.
由于![]() 是两个统计量,因此
是两个统计量,因此![]() 实际上是一个随机区间,它覆盖
实际上是一个随机区间,它覆盖![]() 就是一个随机事件,而
就是一个随机事件,而![]() 就反映了这个区间估计的可信程度;另外,区间长度
就反映了这个区间估计的可信程度;另外,区间长度![]() 也是一个随机变量,
也是一个随机变量,![]() 反映了区间估计的精确程度.我们自然希望反映可信程度越大越好,反映精确程度的区间长度越小越好.但在实际问题中,二者常常不能兼顾.为此,这里引入置信区间的概念,并给出在一定可信程度的前提下求置信区间的方法,使区间的平均长度最短.
反映了区间估计的精确程度.我们自然希望反映可信程度越大越好,反映精确程度的区间长度越小越好.但在实际问题中,二者常常不能兼顾.为此,这里引入置信区间的概念,并给出在一定可信程度的前提下求置信区间的方法,使区间的平均长度最短.
定义 设总体X的分布函数F(x;θ)含有一个未知参数θ,对于给定的α(0<α<1),由样本确定的两个统计量![]() 满足:
满足:![]() ,则称
,则称![]() 为θ的置信度为1-α的置信区间,1-α称为置信度或置信水平,
为θ的置信度为1-α的置信区间,1-α称为置信度或置信水平,![]() 称为双侧置信区间的置信下限,
称为双侧置信区间的置信下限,![]() 称为置信上限.
称为置信上限.
当X是连续型随机变量时,对于给定的α,我们总是按要求![]() 求出置信区间;而当X是离散型随机变量时,对于给定的α,我们常常找不到区间
求出置信区间;而当X是离散型随机变量时,对于给定的α,我们常常找不到区间![]() 使得
使得![]() 恰为1-α,此时我们取区间
恰为1-α,此时我们取区间![]() 至少为1-α且尽可能接近1-α.
至少为1-α且尽可能接近1-α.
若反复抽样多次,每个样本值确定一个区间![]() ,每个这样的区间要么包含θ的真值,要么不包含θ的真值,据Bernoulli大数定律,在这样多的区间中,包含θ真值的概率约为1-α,不包含θ真值的概率约为α,比如,α=0.005,反复抽样1 000次,则得到的1 000个区间中不包含θ真值的区间仅有5个.
,每个这样的区间要么包含θ的真值,要么不包含θ的真值,据Bernoulli大数定律,在这样多的区间中,包含θ真值的概率约为1-α,不包含θ真值的概率约为α,比如,α=0.005,反复抽样1 000次,则得到的1 000个区间中不包含θ真值的区间仅有5个.
例1 设总体X~N(μ,σ2),σ2为已知,μ为未知,X1,X2,…,Xn是来自X的一个样本,求μ的置信度为1-α的置信区间.
解 由前知:![]() 是μ的无偏估计,且有
是μ的无偏估计,且有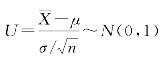 ,
,
据标准正态分布的α分位点的定义有:![]() ,
,
所以μ的置信度为1-α的置信区间为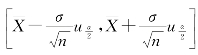 ,简写成
,简写成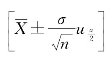 ,
,
比如,α=0.05时,1-α=0.95,查表得:![]() .(https://www.xing528.com)
.(https://www.xing528.com)
又若σ=1,n=16, =5.4,则得到一个置信度为0.95的置信区间
=5.4,则得到一个置信度为0.95的置信区间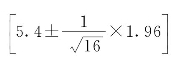 ,即[4.91,5.89].
,即[4.91,5.89].
注意:此时,该区间已不再是随机区间了,但我们可称它为置信度为0.95的置信区间,其含义是“该区间包含μ”这一陈述的可信程度为95%.写成P{4.91≤μ≤5.89}=0.95是错误的,因为此时该区间要么包含μ,要么不包含μ.
若记L为置信区间的长度,则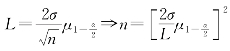 ,从中得知:n增大L减小(α给定),由此可以确定样本容量n,使置信区间具有预先给出的长度.
,从中得知:n增大L减小(α给定),由此可以确定样本容量n,使置信区间具有预先给出的长度.
通过上述例子,可以得到寻求未知参数θ的置信区间的一般步骤为.
(1)寻求一个样本X1,X2,…,Xn的函数(X1,X2,…,Xn;θ);它包含待估参数θ,而不包含其他未知参数,并且U的分布已知,且不依赖于任何未知参数.这一步通常是根据θ的点估计及抽样分布得到的.
(2)对于给定的置信度1-α,定出两个常数a,b,使P{a≤W≤b}=1-α.这一步通常由抽样分布的分位数定义得到.
(3)从α≤W≤b中得到等价不等式![]() ,其中:
,其中:![]() 都是统计量,则
都是统计量,则![]() 就是θ的一个置信度为1-α的置信区间.
就是θ的一个置信度为1-α的置信区间.
下面就正态总体的期望和方差,给出其置信区间.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




