最大似然估计法-概率统计及应用

1.基本思想

若总体X的分布律为P{X=x}=p（x；θ）（密度函数为f（xi，θ）），其中θ=（θ1，θ2，…，θk）为待估参数.

设X1，X2，…，Xn是来自总体X的一个样本，x1，x2，…，xn是相应于样本的一样本值，易知：样本X1，X2，…，Xn取到观测值x1，x2，…，xn的概率为

令

则概率p随θ的取值变化而变化，它是θ的函数，L（θ）称为样本的似然函数（注意：这里的x1，x2，…，xn是已知的样本值，它们都是常数）.如果已知当时使L（θ）取最大值，我们自然认为θ0作为未知参数θ的估计较为合理.

最大似然估计法就是固定样本观测值（x1，x2，…，xn），在θ取值的可能范围内，挑选使似然函数L（x1，x2，…，xn；θ）达到最大（从而概率p达到最大）的参数值作为参数θ的估计值，即，这样得到与样本值（x1，x2，…，xn）有关，常记为，称之为参数θ的最大似然估计值，而相应的统计量称为参数θ的最大似然估计量.这样将原来求参数θ的最大似然估计值问题就转化为求似然函数L（θ）的最大值问题了.

2.具体做法

（1）在很多情况下，p（x；θ）和f（x；θ）关于θ可微，因此据似然函数L（θ）的特点，常把它变为如下形式：，该式称为对数似然函数.由高等数学知，L（θ）与ln L（θ）的最大值点相同.令，i=1，2，…，k，解得θ=θ（x1，x2，…，xn），从而可得参数θ的极大似然估计量为.

（2）若p（x；θ）和f（x；θ）关于θ不可微，则需另寻方法.

例6 设总体X～P（λ），求λ的最大似然估计量.

解 似然函数为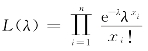　

对数似然函数为　

令，

求得λ的最大似然估计值为，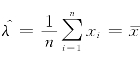

最大似然估计量为.

例7 总体X～E（λ），求λ的最大似然估计量.

解 总体X的概率密度为，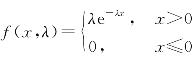

似然函数为　(https://www.xing528.com)

对数似然函数为，

令，有，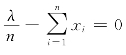

因此，λ的最大似然估计值为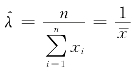，最大似然估计量为.

例8 设X～B（1，p），p为未知参数，x1，x2，…，xn是一个样本值，求参数p的极大似然估计量.

解 因为总体X的分布律为：P{X=x}=px（1-p）1-x，x=0，1，故似然函数为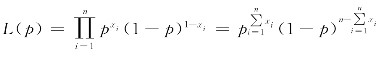，xi=0，1（i=1，2，…，n），

而，

令，解得p的极大似然估计值为，

所以p的极大似然估计量为.

例9 设X～N（μ，σ2），μ，σ2未知，X1，X2，…，Xn为X的一个样本，x1，x2，…，xn是X1，X2，…，Xn的一个样本值，求μ，σ2的极大似然估计值及相应的估计量.

解 因为　

所以似然函数为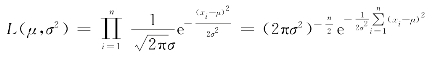　

取对数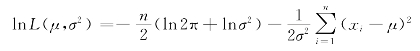　

分别对μ，σ2求导数：

由式，代入式，

所以μ，σ2的极大似然估计值分别为，

μ，σ2的极大似然估计量分别为.