相关系数的定义及性质

定义2 设随机变量X和Y的方差都存在且不为零，X和Y的协方差Cov（X，Y）也存在，则称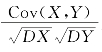为随机变量X和Y的相关系数，记作ρXY，即

如果ρXY=0，则称X和Y不相关；如果ρXY>0，则称X和Y正相关.特别地，如果ρXY=1，则称X和Y完全正相关；如果ρXY<0，则称X和Y负相关.特别地，如果ρXY=-1，则称X和Y完全负相关.

容易验证X和Y的相关系数ρXY有如下性质：

性质1 |ρXY|≤1.

性质2 |ρXY|=1的充分必要条件是：存在常数a，b使得P{Y=a X+b}=1.

由此可见，相关系数定量地刻画了X和Y的相关程度：|ρXY|越大，X和Y的相关程度越大，ρXY=0时相关程度最低.需要说明的是：X和Y相关的含义是指X和Y存在某种程度的线性关系，因此，若X和Y不相关，只能说明X与Y之间不存在线性关系，但并不排除X和Y之间存在其他关系.

对于随机变量X与Y，容易验证下列事实是等价的：

(1)Cov(X,Y)=0;

（2）X和Y不相关；

(3)E(XY)=E(X)E(Y);

(4)D(X+Y)=D(X)+D(Y).

例2 将一颗均匀的骰子重复投掷n次，随机变量X表示出现点数小于3的次数，Y表示出现点数不小于3的次数.(www.xing528.com)

（1）证明：X与Y不相互独立；

（2）证明：X+Y和X-Y不相关；

（3）求3X+Y和X-3Y的相关系数.

证明 由于

因此X和Y不相互独立；

因此，X+Y和X-Y不相关；

于是，3X+Y和X-3Y的相关系数为

注意：（1）随机变量的独立性和不相关性都是随机变量之间的联系“薄弱”的一种反映.“不相关”是一个比“独立”更弱的一个概念.不过对于最常用的正态分布来说，不相关性和独立性是一致的.

（2）二维随机变量，则随机变量X和Y相互独立的充分必要条件是参数ρ=0.且由于ρ=ρXY，因此X与Y相互独立的充分必要条件是X与Y不相关.因此，二维正态随机变量（X，Y）的分布完全由X和Y的数学期望、方差以及X与Y的相关系数所确定.

为了更好地描述随机变量的特征，除了前面介绍过的数学期望、方差、协方差和相关系数等概念之外，我们介绍一种在理论和应用中都起到重要作用的数学特征——矩.