二维正态分布在概率统计应用中

如果二维随机变量（X，Y）的概率密度为

其中μ1，μ2，σ1，σ2，ρ均为常数，且σ1>0，σ2>0，|ρ|<1，则称（X，Y）服从参数为μ1，μ2，σ1，σ2，ρ的二维正态分布，记作.

例2 设（X，Y）的概率密度为

求概率P{（X，Y）∈G}，其中G={（x，y）|x2+y2≤σ2}.

解 依题意，有

如果二维正态分布（X，Y）服从二维正态分布，则（X，Y）关于X和关于Y的边缘分布（下节介绍）都是一维正态分布，且，并且（X，Y）的分布与参数ρ有关.对于不同的ρ，有不同的二维正态分布，但（X，Y）关于X和关于Y的边缘分布都与ρ无关.这一事实表明，仅仅根据（X，Y）关于X和关于Y的边缘分布，一般不能确定随机变量X和Y的联合分布.

习题3.3

1.设二维随机变量（X，Y）具有的概率密度函数

求：（1）分布函数F（x，y）；

（2）概率P{Y≤X}.

2.设（X，Y）的分布函数为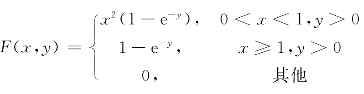，求（X，Y）的概率密度函数f（x，y）.

3.设随机变量（X，Y）的概率密度为(www.xing528.com)

试求：（1）常数k；

(2)P{X<1,Y<3};

(3)P{X<1.5};

(4)P{X+Y≤4}.

4.设二维随机变量（X，Y）在区域G上服从均匀分布，其中G是曲线y=x2和直线y=x所围成的区域，试求：

（1）（X，Y）的联合概率密度f（x，y）；

(2)P{Y<X}.

5.设二维随机变量（X，Y）服从D={（x，y）|0≤x≤1，0≤y≤x}上的均匀分布，试求：

（1）（X，Y）的概率密度；

(2)P{X+Y≤1};

(3)P{Y≤X2}.