方差性质解析|概率统计及其应用

设C为常数，随机变量X，Y的方差都存在.关于方差有如下性质：

性质1 D（C）=0.

事实上，D（C）=E{[C-E（C）]2}=0.

性质2 D（CX）=C2D（X）.

事实上，D（CX）=E{[CX-E（CX）]2}

=C2E{[X-E(X)]2}=C2D(X).

性质3 D（X+C）=D（X）.

事实上，D（X+C）=E{[（X+C）-E（X+C）]2}

=E{[X+C-E(X)-C]2}

=E{[X-E(X)]2}

=D(X).

性质4 如果随机变量X，Y相互独立，则

D(X+Y)=D(X)+D(Y)

事实上，

D(X+Y)=E{X-E(X)+[Y-E(Y)]}2

=E[X-E(X)]2+2E{[X-E(X)][Y-E(Y)]}+E[Y-E(Y)]2

=D(X)+2E{[X-E(X)][Y-E(Y)]}+D(Y)

注意到X和Y相互独立，因此X-E（X）和Y-E（Y）也相互独立，由数学期望的性质，有

E{[X-E(X)][Y-E(Y)]}=E[X-E(X)]·E[Y-E(Y)]=0

于是　D（X+Y）=D（X）+D（Y）

性质5 随机变量X的方差D（X）=0的充分必要条件是：X以概率1取值常数C，即

P{X=C}=1

下面的结论在数理统计中是很有用的.

例3 设X1，X2，…，Xn相互独立并且服从同一分布，若

E(Xi)=μ, D(Xi)=σ2

记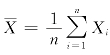，证明：E（）=μ.

证明 由数学期望的性质，

又由独立性和方差的性质知

于是.

若用X1，X2，…，Xn表示对物体重量的n次重复测量的误差，而σ2为误差大小的度量，公式表明n次重复测量的平均误差是单次测量误差的，也就是说，重复测量的平均精度要比单次测量的精度高.

问题思考：（生产规模的确定）一生产企业生产某产品的日产量可以是600，700，800和900件，根据历史资料知这种产品的日需求量为600，700，800，900件的概率分别为0.1，0.4，0.3，0.2，各种规模生产时的获利Xi（i=1，2，3，4）如下表（利润单位：百元）.根据期望利润最大的原则确定应采用哪种规模生产.

附：几种常用的概率分布表

习题2.6

1.设随机变量X服从0—1分布，其分布律为

P{X=0}=1-p,P{X=1}=p

求E（X），D（X）.

2.设随机变量X的概率分布为

求D（X）.

3.设随机变量X的密度函数为.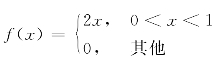

求X的方差D（X）.

4.设随机变量X的密度函数为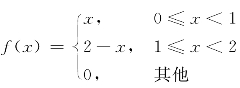，求E（X2）及X的方差D（X）.

5.一批零件中有9个合格品与3个次品，在安装机器时，从这批零件中任取一个，如果取出的是次品就不放回去，求在取得合格品以前，已经取出的次品数的数学期望和方差.

总复习题二

1.同时抛掷2枚硬币，以X表示出现正面的枚数，求X的分布律.

2.一口袋中有6个球，依次标有数字3，6，6，9，9，9，从口袋中任取一球，设随机变量X为取到的球上标有的数字，求X的分布律以及分布函数.

3.一袋子中有5个白色乒乓球，编号分别1，2，3，4，5，从中随机地取3个，以X表示取出的3个球中最大号码，写出X的分布律以及分布函数.

4.已知随机变量X的分布函数为

求概率P{1<X≤2}.

5.设离散型随机变量X的分布律为

(1)P{X=i}=a(1/4)i,i=1,2,3;

(2)P{X=i}=a(1/4)i,i=1,2,….

分别求出上述各式中的a.

6.已知连续型随机变量X的分布函数为

求常数a和b.

7.已知连续型随机变量X的概率密度为

求常数k和概率P{-1<X<1}.

8.已知连续型随机变量X的概率密度为

求X的分布函数.(www.xing528.com)

9.连续不断地掷一枚均匀的硬币，问：至少掷多少次才能使正面至少出现一次的概率不少于0.99？

10.设每分钟通过某交叉路口的汽车流量X服从泊松分布，且已知在一分钟内无车辆通过与恰有一辆车通过的概率相同，求在一分钟内至少有两辆车通过的概率.

11.设每次射击不命中目标的概率为0.001，共射击1 000次，若X表示命中目标的次数，

（1）求随机变量X的分布律；

（2）计算至少有两次命中目标的概率.

12.设随机变量X的密度函数为f（x）=A e-|x|，-∞<x<+∞.

（1）求常数A；

（2）求X的分布函数；

（3）求P{0<X<1}.

13.证明：函数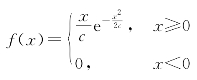 （c为正常数）是某个随机变量X的密度函数.

14.设随机变量X的概率密度为，求：

（1）X的分布函数；

(2)P{X≥200}.

15.某种显像管的寿命X（单位：h）的概率密度为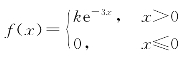.求：

（1）常数k的值；

（2）寿命小于1 000 h的概率.

16.设X～N（0，1），求：

(1)P{X≤1.96};

(2)P{X≤-1.96};

(3)P{X>1.96};

(4)P{-1<X≤2};

(5)P{|X|≤1.96}.

17.设X～N（1.5，4）.求：

(1)P{X≤3.5};

(2)P{X≤-4};

(3)P{X>2};

(4)P{|X|<3}.

18.设随机变量X服从参数为λ=1的泊松分布，随机变量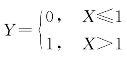，求随机变量Y的分布律.

19.设随机变量X的概率密度为

对X独立重复观察三次，求至少有两次观察值不大于0.5的概率.

20.已知电源电压X服从正态分布N（220，252），在电源电压处于X≤200 V，200 V<X≤240 V，X>240 V三种情况下，某电子元件损坏的概率分别为0.1，0.01，0.2.

（1）求该电子元件损坏的概率α；

（2）已知该电子元件损坏，求电压在200～240 V的概率β.

21.假设自动生产线加工的某种零件的内径服从正态分布N（11，1），内径小于10或大于12为不合格品，其余为合格品，销售每件合格品获利，销售每件不合格品则亏损，若销售利润Y与销售零件的内径X有下列关系

求Y的分布律.

22.已知随机变量X的分布律为

求Y=X2的分布律.

23.设随机变量X服从[0，1]上的均匀分布，求Y=X2的概率密度.

24.在下列句子中随机取一个单词，以X表示取到的单词所包含的字母的个数，写出X的分布律，即求E（X）.

“THE GIRL PUT ON HER BEAUTIFL RED HAT”

25.某商场计划于5月1日在户外搞一次促销活动，统计资料表明，如果在商场内搞促销活动，可获得经济效益3万元；在商场外搞促销活动，如果不遇到雨天可获得经济效益12万元，遇到雨天则带来经济损失5万元；若前一天的天气预报称活动当日有雨的概率为40%，则商场应如何选择促销方案.

26.一批产品中有16个合格品和4个废品.装配仪器时，从这批零件中任取一个，如果取出的是废品，则扔掉后重新任取一个.求在取到合格品前已经扔掉的废品数的数学期望.

27.一台设备由三大部件构成，在设备运转的过程中各部件需要维护的概率分别为0.1，0.2，0.3.假设各部件的状态都是相互独立的，以X表示同时需要调整的部件数，求E（X）.

28.据统计，一位60岁的健康者（一般体检未发生病症），在5年内仍然活着或自杀的概率为p（0<p<1，p为已知），在5年之内非自杀死亡的概率为1-p，保险公司开办5年人寿保险，条件是参加者需交纳人寿保险费用a元（a已知），若在5年内死亡，公司赔偿b元（b>a），应如何确定b才能使公司可期望获益？若有m人参加保险，公司可期望从中受益多少？

29.已知投资某一项目的收益率X是一随机变量，其分布律为

一位投资者在该项目上投资了10万元，求他预期获得多少收益.

30.已知随机变量X的概率密度为

求：（1）常数a；（2）E（X）.

31.一工厂生产的某种设备的寿命X（以年计）服从指数分布，概率密度为

工厂规定，出售的设备若在一年之内损坏可予以调换.若工厂售出一台设备盈利100元，调换一台设备厂方需花费300元.试求厂方出售一台设备净盈利的数学期望.

32.设随机变量X的分布律为

求：（1）常数c；（2）E（X）；（3）E（X2）.

33.设电压（以V计）X～N（0，9），将电压施加于检波器，其输出电压为Y=5X2，求输出电压Y的均值.

34.设随机变量X的概率密度为

求：（1）E（X）；（2）D（X）.

35.已知随机变量X的分布律为

求D（X）.