设C为常数，随机变量X，Y的数学期望都存在.关于数学期望有如下性质成立：
性质1 E（C）=C.
性质2 E（CX）=CE（X）.
性质3 E（X+Y）=E（X）+E（Y）.
性质4 如果随机变量X和Y相互独立，则E（XY）=E（X）E（Y）.
这里只就连续型随机变量的情形对性质3和性质4给出证明，对于离散型随机变量情况，请读者自行完成.
证明 设二维连续型随机变量（X，Y）的概率密度为f（x，y），（X，Y）关于X和关于Y的边缘概率密度为fX（x）和fY（y），则有
如果X和Y相互独立，则f（x，y）=fX（x）fY（y），有
例7 设随机变量X和Y相互独立，且各自的概率密度为
求E（XY）.
解 由性质3得(www.xing528.com)
问题思考：（最少进货量）设某商品每周的需求量X～U（10，30），而经销商进货量为区间（10，30）中某一个整数，商店每销售一件商品可获利500元.若供大于求，则削价处理，每处理一件商品亏损100元；若供不应求，则可从外部调剂供应，此时每件商品仅获利300元.为使商店所获利润期望值不少于9 280元，试确定最少进货量.
习题2.5
1.设随机变量X的分布律为
求E（X），E（X2），E（3X2+5）.
2.设连续性随机变量X的概率密度为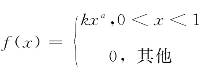
，其中k，a>0，又已知E（X）=0.75，求k，a的值.
3.设随机变量X的概率密度为
，求E（X）.
4.一工厂生产的某种设备的寿命X（以年计）服从指数分布，概率密度为f（x）=
，工厂规定，出售的设备若在售出一年之内损坏可予以调换.若工厂售出一台设备盈利100元，调换一台设备厂方需花300元.试求厂方出售一台设备净盈利的数学期望.
5.设随机变量X的概率密度为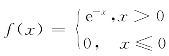
，求：
（1）Y=2X的数学期望；（2）Y=e-2X的数学期望.
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
