随机变量及其应用-概率统计及其应用

在许多随机试验中，试验的结果可以直接用一个数值来表示，不同的结果对应着不同的数值.

引例1 投掷一颗骰子，观察出现的点数，可能的结果分别是1，2，3，4，5，6这六个数值.如果我们用一个变量X表示出现的点数，那么试验的所有可能结果都可以用X的取值来表示，即

显然，X是一个变量，它取不同的数值表示试验中可能发生的不同结果，并且X是按一定概率取值的，如{X=5}表示事件“出现5点”，且.

引例2 100件商品中有2件次品，任取两件，其中次品数X可以随机地取0，1，2这三个数值，即

显然，X是一个变量，且.

有些试验的结果本身与数值无关，但同样可以用某个变量的取值来表示.

例如抛掷一枚硬币，它的可能结果为“出现正面”或“出现反面”.我们引进变量X，用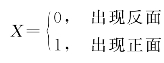，且P{X=0}=P{X=1}=0.5.(www.xing528.com)

一般地，我们有下面的定义.

定义1 设随机试验E的样本空间为Ω，如果对于每一个ω∈Ω，都有唯一的实数X（ω）与之对应，则称X=X（ω）为随机变量.

引入随机变量以后，就可以用随机变量来表示随机试验中的各种事件.例如在上面的引例2中，事件“至少有1件次品”可以用{X≥1}来表示，事件“至少2件次品”可以用{X≥2}来表示.可见，随机变量是一个比随机事件更宽泛的概念.

随机变量概念的产生是概率论发展史上的重大事件.引入随机变量的概念后，概率论的研究中心就从随机事件的研究转移到随机变量及其取值规律的研究，概率论的发展也从古典概率时期过渡到分析概率时期.

随机变量依其取值的特点分为离散型和非离散型两类.如果随机变量X的所有可能取值为有限个或可数无穷多个，则称X为离散型随机变量，否则称为非离散型随机变量.在非离散型随机变量中最重要的是连续型随机变量.