政府与企业的安全生产管理模式研究及稳定性分析

在模型中，假定博弈参与者有两方，即政府和企业。政府的行为包括管制与不管制两种，企业的行为包括管理和不管理两种。政府在管制中的收益主要有两种：预防性管制收益和事故发生后管制（简称事后管制）收益。预防性管制是指政府为了避免事故发生而进行的管制行为，而事后管制是指在事故发生后，政府对企业和相关责任人进行的惩罚性的管制行为。为简化分析，可以认为企业进行的安全管理是有效的，即只要进行了安全管理，企业就不会发生相应的生产事故。而当企业不进行安全生产管制时，企业将会以一定的比例发生生产事故。政府和企业的非合作重复博弈矩阵如下表所示：

表5.1　政府和企业安全生产管制博弈收益矩阵

在上述矩阵中，表示企业的生产收益，表示企业配合政府管制花费的成本，表示企业在政府安全生产监管部门督促下进行的安全生产投资额，表示企业在事故前的安全生产检查行为中收取的罚金，表示企业在事故后安全生产管制行为中收取的罚金，表示政府在事故前检查行为中花费的费用，表示政府在事故后管制行为中花费的费用，表示事故发生率，表示企业的潜在事故损失，表示政府在企业进行管理的前提下由于其管制行为得到的收益（因为政府的管制行为可以给社会及其上级机关留下勤勉的印象，故而会得到相应的收益），表示政府在企业不进行管理的前提下由于其管制行为得到的收益（在这种情况下，由于政府通过其管制行为减少了社会的安全生产隐患，故而，其得到的收益应该更大，即。

由Malthusian 动态方程原理可知，当策略的增长率等于它的相对适应度，只要采取这个策略的个体适应度比群体的平均适应度高，随着时间推移这个策略就会增长。基于此种原理，本模型的动力学模型可以构造过程如下：

①参与者政府采用策略和的平均支付为：

②参与者政府的混合策略平均支付为：

③参与者企业采用策略和的平均支付为：

④参与者企业的混合策略平均支付为：

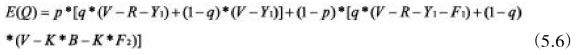(www.xing528.com)

则相应的系统方程如下所示：

化简得：

令（5.9）式和（5.10）等于0，在平面，可得演化博弈的5 个均衡点（0，0），（0，1），（1，0），（1，1），（假定，之所以做这些假设，主要是因为：①一般而言，政府勤政的收益会大于其进行安全生产管制的费用以保持政府进行管制行为的动力；②之所以设定，是因为中小企业的安全生产风险较大，因此值较大，另外，因为中小企业经常发生生产事故，故而政府针对其事故收取的罚金的值较大；③之所以设定，主要是由于生产事故存在或然性且安全生产投资收益具有滞后性，从而，可以认为，对大多数企业而言，在一段较长的时期内，都会满足的条件）。

根据Friedman 提出的方法，对于一个由微分方程系统描述的群体动态，其均衡点的稳定性，是由这个系统得到的雅可比（Jacobian）矩阵的局部稳定分析得到的。下面我们使用Jacobian矩阵的局部稳定分析方法来研究由方程（5.9）和（5.10）组成的系统的稳定性，具体结果如表5.2所示：

表5.2　局部稳定性分析结果

在表5.2中，由于，将式带入式中，故而，。从表（5.2）可以看出，点、点为演化稳定点，点和点为演化不稳定点，点为鞍点。图5.1反映了政府与企业交往的动态演化过程。

图5.1　系统动态演化图