10.3.3.1 控制方程
模型描述污染物对流扩散输移方程为
式中 C——污染物浓度，kg/m3；
Dx，Dy——x、y方向上的水平扩散系数，m2/s；
vx，vy——x、y方向上的流速矢量，m/s；
S——源汇项，表示污染物的吸附、降解或沉降，kg/（m3·s）。
式中 t——计算时段，s；
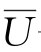——按深度平均的流速矩阵，m/s；
AX、AY——系数矩阵；
u，v——ξ、η方向的流速，m/s。
10.3.3.2 定解条件
1.初始条件
C(x,y,t)=C0(x,y) (10.22)
式中 C0（x，y）——已知的初始浓度，kg/m3。
2.边界条件
闭边界：流量和扩散均为0，且输移为零：
开边界：即水——水边界，可以选择随时间变化或不随时间变化两种。在入流时C=C（t），液体边界浓度在出流时选择自由出流边界：
10.3.3.3 模型求解
在水质模拟研究中，假定剖分所得的每一个网格单元是一个理想混合器，各单元通过交换界面联结，使得概化后的河流成为由N个串联的混合器构成的系统。第i个单元在单位时间内输运的平衡方程为
ΔM=ΔMqi+ΔMEi+ΔMKi (10.23)
式中 ΔM——物质累计量，kg；(www.xing528.com)
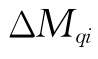——对流输运差值，kg；
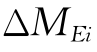——扩散输运差值，kg；
——生化衰减量，kg。
下面分述各项内容的计算方法。
1.随水流输运量（ΔMqi和ΔMEi）
Delwaq模型根据控制体积法，采用迎风差分格式，离散方程得到下式：
式中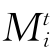
——t时刻i单元中物质质量，kg；
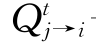——t时刻从j单元流向i单元的流量，m3/s；
——t时刻从i单元流向j单元的流量，m3/s；
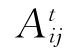——t时刻i单元和j单元交界面的面积，m2；
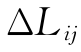——单元i和单元j中心点距离，m；
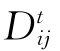——t时刻i单元和单元j中心点距离，m；
ΔM——交换过程中物质质量损失，kg。
2.生化衰减量ΔMKi
生化衰减量ΔMKi计算公式为
ΔMKi=-KVC (10.25)
式中 K——衰减系数，对于降解的物质取正号，聚集的物质取负，降解和聚集都发生的取二者之和；
V——Δt时段内单元的平均水体体积，m3；
C——Δt时间段内污染物的平均浓度值，kg/m3。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
