10.3.2.1 控制方程
模型采用不可压缩流体、浅水、Boussinnesq假定下的Navier-Stokes方程，忽略温度变化对流场和垂向动量方程中垂向加速度的影响。
在水平方向上，采用Delft3D-Flow提供的正交曲线坐标（ε，η）
式中 λ——经度；
ϕ——纬度；
R——地球半径（6370km）；
Gξξ，Gηη——用于转换曲线到直角坐标的系数；
ξ，η——正交曲线坐标的两个方向。
在垂直方向上，采用σ坐标，定义如下：
式中 σ——垂向尺度坐标，无量纲；从水底到自由水面，σ的变化范围为（-1，0）。
z——空间高度，m；
ζ——参照水空间（z=0）以上的水位，m；
d——低于参照水空间的水深，m；
H——总水深，m。
1.连续方程
式中 Q——单位面积由于排水、引水、蒸发或降雨等引起的水量变化，即总的源或汇，m/L；
u，v——ξ、η方向上的速度分量，m/s；
qin，qout——单位体积的局部源（流入量）、局部汇（流出量），L/s；
P——进入水量（降水量、引入水量等），m/s；
E——出去水量（蒸发量、引出水量），m/s。
2.动量方程
水平ξ方向上：
水平η方向上：
式中 u，v——表示在正交曲线坐标系下ξ、η两个方向上的速度分量；
fv——科里奥利（Coriolis）参数（惯性频率），1/s；
Pη——η方向的净水压力梯度，kg/（m2·s2）；
Fξ——ξ方向上的紊流动量通量，m/s2；
Mξ——ξ方向上的动量源或汇，m/s2。
10.3.2.2 模型定解条件(www.xing528.com)
1.初始条件
式中 t——时间，s；
其余符号含义同前。
当t=0时，流场是静止的，亦即参照水空间以上的水位和速度分量均为零。
2.边界条件
（1）运动边界。在σ坐标系中，自由水面（σ=0）和水底（σ=-1）不具渗透性：
（2）底边界。
式中 τbξ，τbη——底部切应力在ξ，η方向上的分量，底部切应力是水流和风共同作用的结果，kg/ms2。
（3）表面边界。
式中 θ——风力形成的角度。
风应力大小的计算公式为
式中 ρa——空气密度，kg/m3；
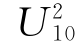——高于自由表面10m处的风速，m/s；
Cd——风的拖曳系数，其大小取决于风速、随风速的增加而相应的水面粗糙度，无量纲。
（4）开边界。在水——水交界面设置开边界，模型有以下四种开边界条件可供选择：水位开边界：
ζ=Fζ(t) (10.14)
流速开边界：
U=FU(t) (10.15)
流量开边界：
Q=FQ(t) (10.16)
Riemann不变式开边界：
上述F（t）由实测资料确定，选择相对应的开边界类型。模型允许将边界分段处理，每段给定端点上的边界过程，中间点采取线性插值的方法计算。对于这四类开边界，假设水流与开边界是垂直正交的。
（5）闭边界。在水——陆交界面设置闭边界，垂直方向流速为零：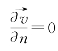
对于大范围的区域模拟，闭边界的剪切力影响可以忽略不计，采取自由滑移边界条件。
10.3.2.3 模型求解方法
模型采用有限差分法求解数学模型，利用正交曲线网格对空间进行离散，因此，对原偏微分方程组的求解就转换为对正交曲线网格上的离散点上的变量值求解，模型采用ADI算法求解（交替方向隐式差分方法）：将一个时间步长进行剖分分成两步，每一步为1/2个时间步长，前半个步长对X进行隐式处理，后半步则对Y方向进行隐式处理。ADI算法的矢量形式如下：
前半步：
后半步：
其中：
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
