扩散系数是研究污染质或溶质的一个重要参数，根据溶质的扩散系数可以计算溶质在不同时段、不同条件下的分布特征，扩散系数的计算方法很多。但对于湖海来讲，由于很难建立对照点，观测扩散也比较困难，因此采用相对扩散的概念。根据溶质运移的溶质扩散带（晕）计算相对扩散系数，即根据扩散范围随时间的变化计算扩散系数。
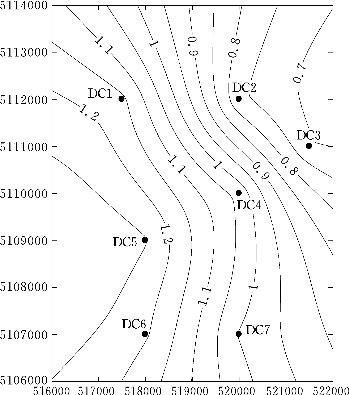
图4.51 模拟实验氟浓度曲线图（6天）（单位：mg/L）
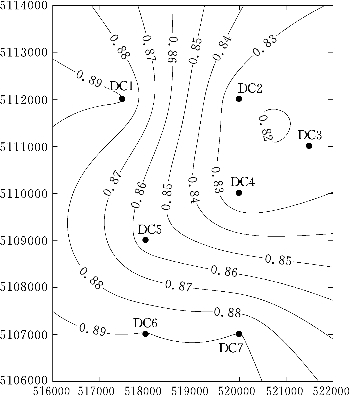
图4.52 模拟实验氟浓度曲线图（12天）（单位：mg/L）
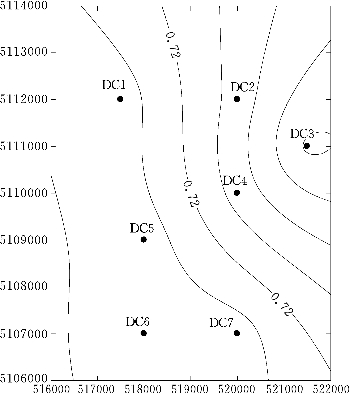
图4.53 模拟实验氟浓度曲线图（21天）（单位：mg/L）
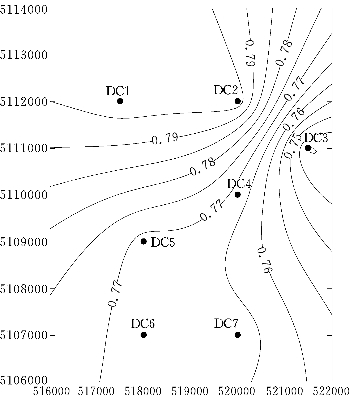
图4.54 模拟实验氟浓度曲线图（28天）（单位：mg/L）
根据环境水力学的诸多研究成果[119]，经多次固定断面观测后可以看出紊动扩散现象的特征，把多次观测的浓度分布的重心叠合起来，它与高斯分布非常接近。认为水流扩散带随着纵向距离x的增长而逐渐放宽，水流扩散带的浓度分布状态和扩散系数有着极为密切的关系，由此得到水流扩散带的浓度分布状态和扩散系数计算公式。
由于洋沙泡水库深度较浅，认为氟在垂向上瞬间达到均匀分布，因此不考虑垂向的浓度分布，则扩散系数计算的数学模型应用二元扩散方程，扩散方程为
根据溶质扩散带的分布，则有
其中
则
(www.xing528.com)
式中 t——扩散时间，s；
σx、σz——水流扩散带测定物浓度在水面上沿着两个水平轴向x、z的标准偏差；
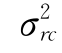——综合方差；
Ex——纵向扩散系数，m2/s；
Ez——横向扩散系数，m2/s；
C——溶质的浓度，mg/L；
x——入水口到取样点的x方向水平距离，m；
z——入水口到取样点的z方向水平距离，m。
由于洋沙泡水库水深不足2m，水流进入洋沙泡后，可以认为是瞬间混合。同时水槽模拟实验中深度较小，水流在垂向上瞬间混合，因此不考虑垂向浓度分布，作为二维考虑。
根据水质模拟实验结果，利用还原计算后的实际位置和数据及上述公式计算扩散系数。采用横向3个系列、纵向2个系列，进行计算。z方向（即横向）采用DC1、DC2（1-2），DC3、DC4、DC5（3-5），DC6、DC7（6-7）构建3个计算系列，计算横向扩散系数Ex，x方向（即纵向）采用DC2、DC4、DC7（2-7），DC1、DC5、DC6（1-6）构建2个计算系列，计算纵向扩散系数Ez。
根据水质模拟结果，计算出相应的横向扩散系数和纵向扩散系数。横向扩散系数值在0.555～0.00001m2/s之间，纵向扩散系数值在18.429～0.00001m2/s之间。
为消除计算结果中特大值和特小值的影响，剔除不合理因素，又分别计算了每个系列的中值和平均值；再计算每个系列的中值与平均值的综合均值，然后计算几个系列的综合均值，并以此值作为最终的计算结果。扩散系数的计算结果见表4.13～表4.14。
表4.13 横向扩散系数计算成果表
表4.14 纵向扩散系数计算成果表
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
