ANSYS14.0应用实例：线弹性静力学求解

线弹性静力学问题可以用平衡方程、变形协调方程、几何方程、本构方程（应力-应变关系）、边界条件和结构外载荷来描述。因为虚功原理满足变形体的平衡方程和变形协调方程，并且在式（8-15）推导过程中，引入了小变形和线弹性的应力-应变关系，所以式（8-15）能够保证在每个单元内部满足平衡方程、变形协调方程和线弹性应力-应变关系。为了能够求解线弹性静力学问题，还需要引入边界条件来消除总体刚度矩阵的奇异性，再结合给定的结构外载荷就可以完成对线弹性问题的求解。

由式（8-15）可知，在有限元求解过程中，是以结构中节点位移作为基本未知量，进行求解的。一旦求解出节点位移，就可以通过式（8-4）得出单元应变，再根据如下的线弹性本构方程，得出单元应力。

式中，{σ}为应力分量，即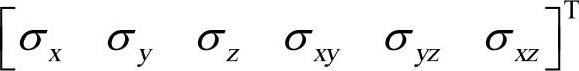在ANSYS软件里以S代替σ形式出现；[D]为应力-应变矩阵。

图8-2所示为单元应力矢量图。ANSYS程序中规定正应力和正应变拉伸时为正，压缩时为负；正剪切应变为使直角减小方向，负剪切应变为使直角增大方向。

式（8-16）还可以被写为以下形式：

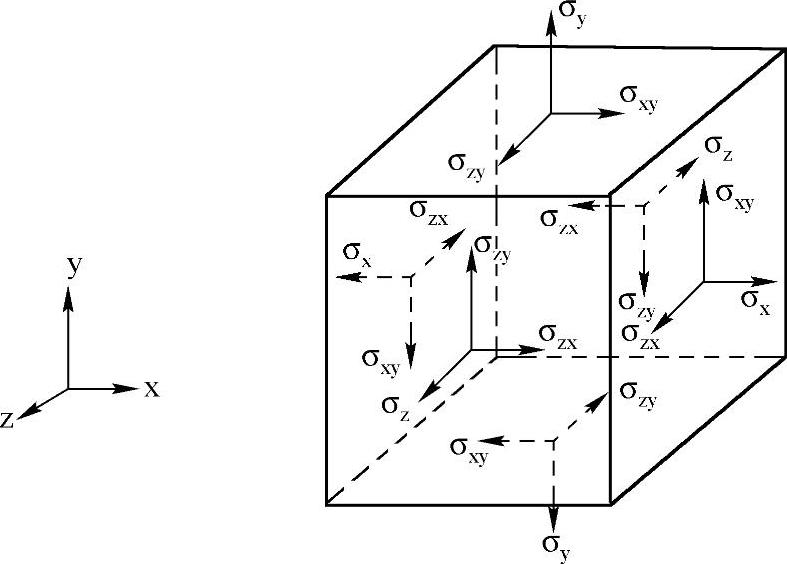
图8-2 单元的应力矢量图

柔度矩阵的定义：

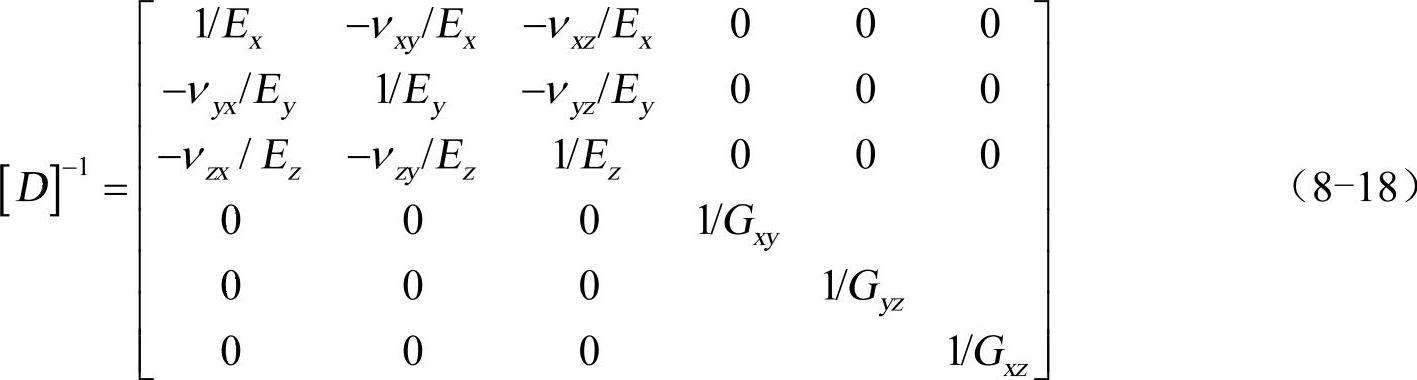
式中，E_x为x方向上的杨氏模量；ν_xy为主泊松比；ν_yx为次泊松比；G_xy为xy平面上的剪切模量。此外，[D]⁻¹是对称矩阵，因此

由式（8-18）～式（8-21），可知(www.xing528.com)

ν_xy、ν_yz、ν_xz、ν_yx、ν_zy和ν_zx是不独立的，因此程序中必须输入3个主泊松比

ν_xy、ν_yz和ν_xz（以PRXY，PRYZ，and PRXZ标记输入）或3个次泊松比ν_yx、ν_zy和ν_zx（以NUXY，NUYZ，and NUXZ标记输入）。通过以下操作来实现在ANSYS中的参数输入。

GUI：Main Menu︱Preprocessor︱Material PropsMaterial Models︱Material Models Available︱Structural︱Linear︱Elastic︱Orthotropic，弹出图8-3所示的“Linear Orthotropic Properties for Material Number 1（线弹性正交各向异性材料模型参数输入）”对话框。通过操作对话框中的Choose Poisson’s Ratio选项，来选择使用泊松比的类型，即选择主泊松比还是次泊松比，然后在面板6个输入框中分别输入弹性模型（EX、EY、EZ），泊松比（PRXY、PRYZ、PRXZ）和剪切模量（GXY、GYZ、GXZ）。

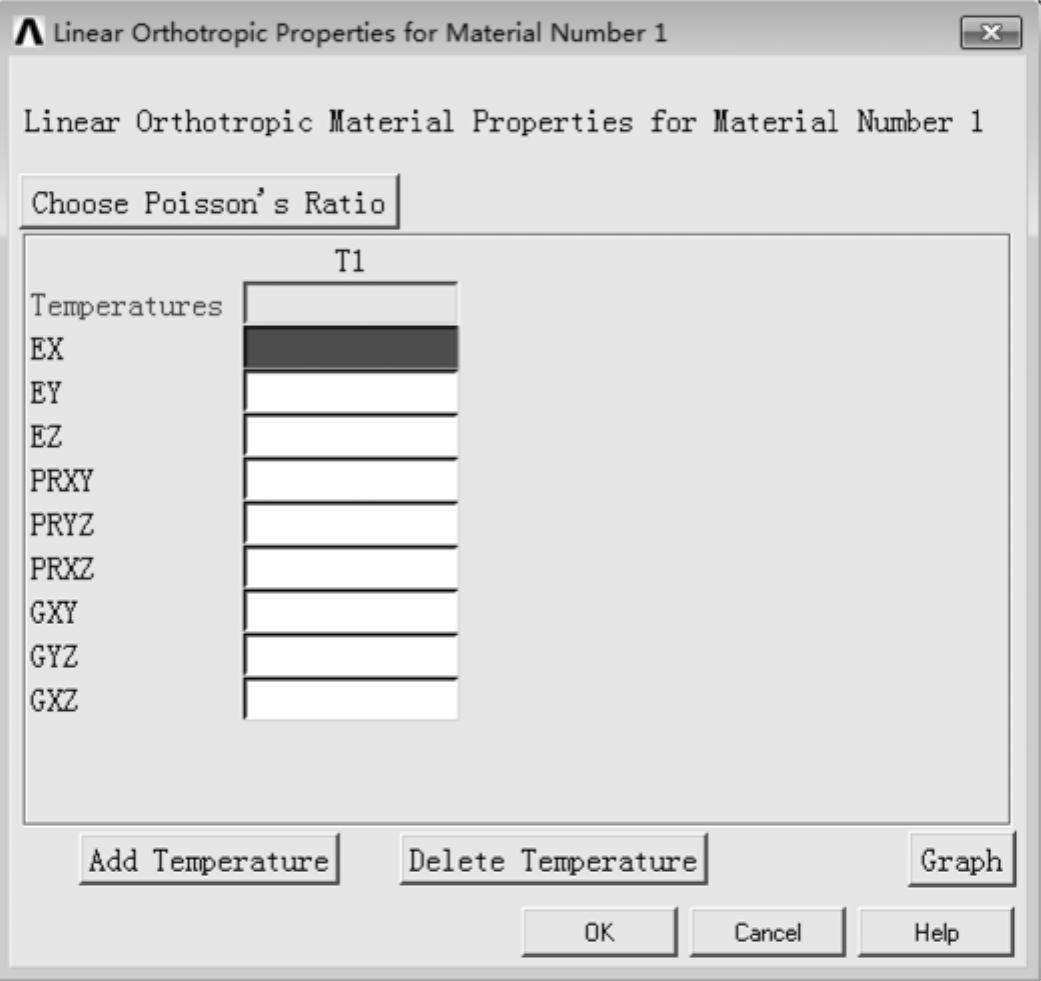
图8-3 “线弹性正交各向异性材料模型参数输入”对话框

对于各向同性材料，各方向上的泊松比和弹性模量相同，因此在数据输入中没有区别。其输入方法如下。

GUI：Main Menu︱Preprocessor︱Material PropsMaterial Models︱Material Models Available︱Structural︱Linear︱Elastic︱Orthotropic，弹出图8-4所示的“Linear Isotropic Properties for Material Number 1（线弹性各向同性材料模型参数输入）”对话框。在对话框的EX输入框中输入弹性模量；PRXY输入框中输入主泊松比。

由于在计算各向同性材料时，可利用下式计算剪切模量：

所以对于各向同性的线弹性材料不需要输入剪切模量。

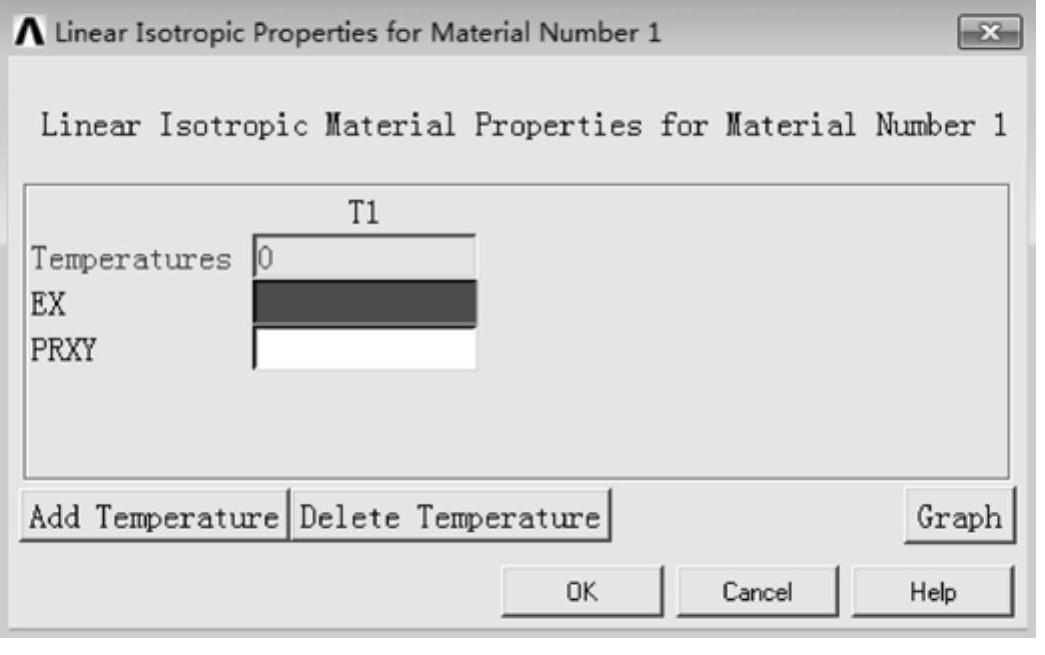
图8-4 “线弹性各向同性材料模型参数输入”对话框