ANSYS14.0矩阵导出示例

虚功原理：当应变发生微小变化时，内部产生的应变能与外载荷对其做功相等，即

δU=δV （8-1）

式中，U为应变能；V=V₁+V₂+V₃为外力做功；δ为虚位移算子。

虚应变能为

式中，{ε}为应变矢量；{σ}为应力矢量；vol为单元体积。

假定材料和几何是线性的，则

应变与节点位移的关系：

{ε}=[B]{u} （8-4）

式中，[B]为应变位移矩阵，取决于单元的形函数；{u}为节点位移矢量。

假定下面的计算在笛卡儿坐标系中，把式（8-4）代入式（8-3），得

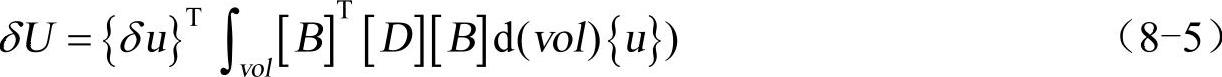
接下来，考虑外力的虚功。首先考虑惯性影响：

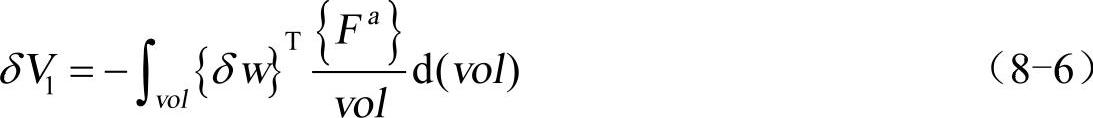
式中，[w]为每个点上的位移矢量；{F^a}为产生加速度的力矢量。

然后考虑牛顿第二定律：

式中，ρ为密度，可以利用MP命令输入，t为时间。

单元内部的位移与节点位移关系为

{w}=[N]{u} （8-8）

式中，[N]为形函数矩阵。

假设单元密度为常量，并利用式（8-6）～式（8-8），得(www.xing528.com)

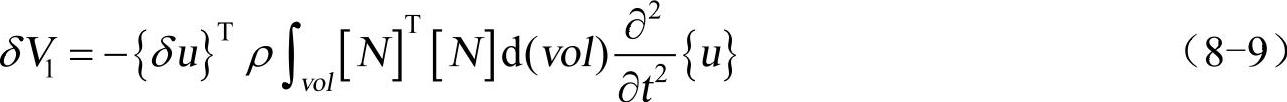
压力矢量形成的外力功为

式中，{P}为使用的压力矢量（通常仅一个非零分量）；area_p为压力的作用面。

由式（8-8）和式（8-10），得

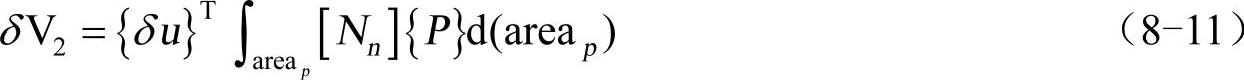
除非另有说明，否则压力总是施加在单元的外表面并且总垂直于曲面。

第3种外力功为节点力作的功：

式中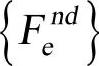，为施加在单元上的节点力。

最终，由式（8-5）、式（8-8）、式（8-8）和式（8-12），得

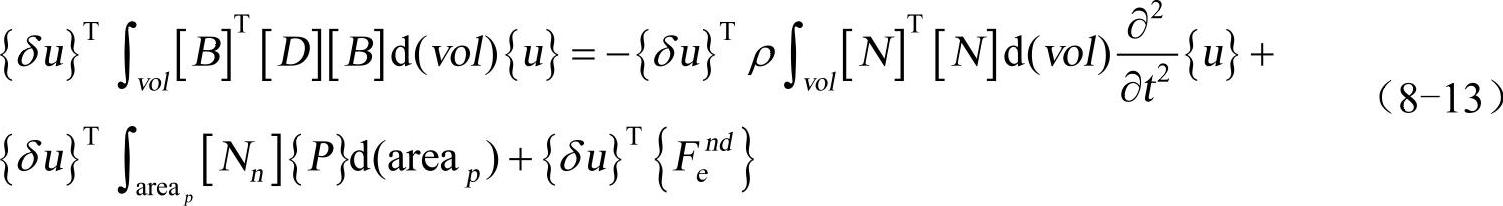
考虑到{δu}是一系列的虚位移矢量，因此式（8-13）可以化简为

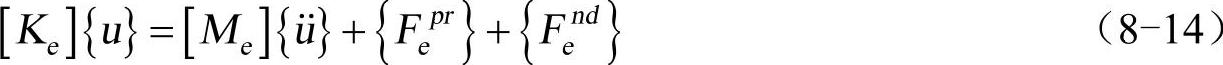
式中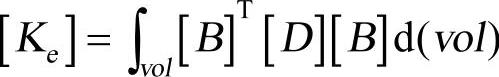，为单元刚度矩阵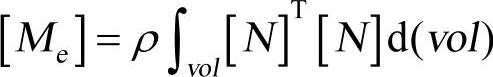；为单元质量矩阵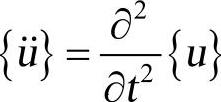；为加速度矢量（如重力加速度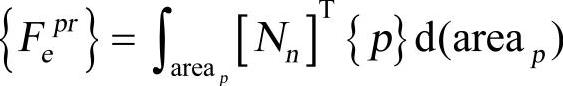）；为单元压力矢量。

式（8-14）为单元基本的平衡代数方程，则线弹性静力学结构的总体平衡方程为

[K]{u}={F} （8-15）

式中，[K]为结构总体刚度矩阵；{u}为结构节点位移矢量；{F}为结构载荷矢量，包括节点载荷、压力载荷和惯性载荷。

以上所讨论的矩阵和载荷矢量都是“一致性”的，即使用同样的形函数来确定。但其他的形式也是存在的，如质量矩阵为对角阵则要使用（LUMPM，ON）来形成集中质量。大多数集中质量矩阵中不包含转动自由度。如果要求删除转动自由度，这样形成的矩阵或载荷矢量称为“缩减形式”。因此使用缩减型压力载荷矢量不会产生力矩。使用一致性压力载荷矢量在结构中会产生错误的内力矩。例如，一个薄的圆柱体承受内压作用并且使用不规则壳单元分析，如图8-1所示，可以看出一致性压力载荷矢量在两个相邻的、尺寸不同的单元上产生了不正确的力矩。

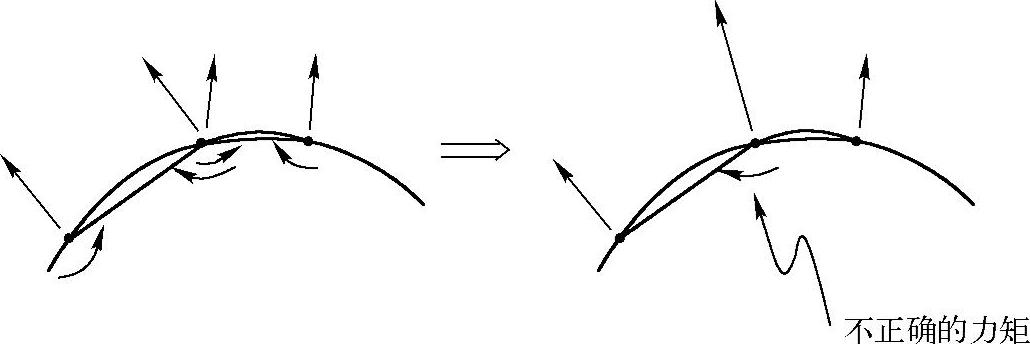
图8-1 一致性压力载荷的影响