翘曲系数检查方法-ANSYS14.0实例

四边形壳单元和六面体单元、楔形体的四边形表面、金字塔单元的表面需要计算和检测翘曲系数。表2-7给出了单元翘曲系数的限制。大的翘曲系数表明潜在的单元规划不能很好地执行或暗示网格可能产生裂缝。

表2-7 翘曲系数的限制

1.四边形壳单元翘曲系数的计算

计算步骤如下：

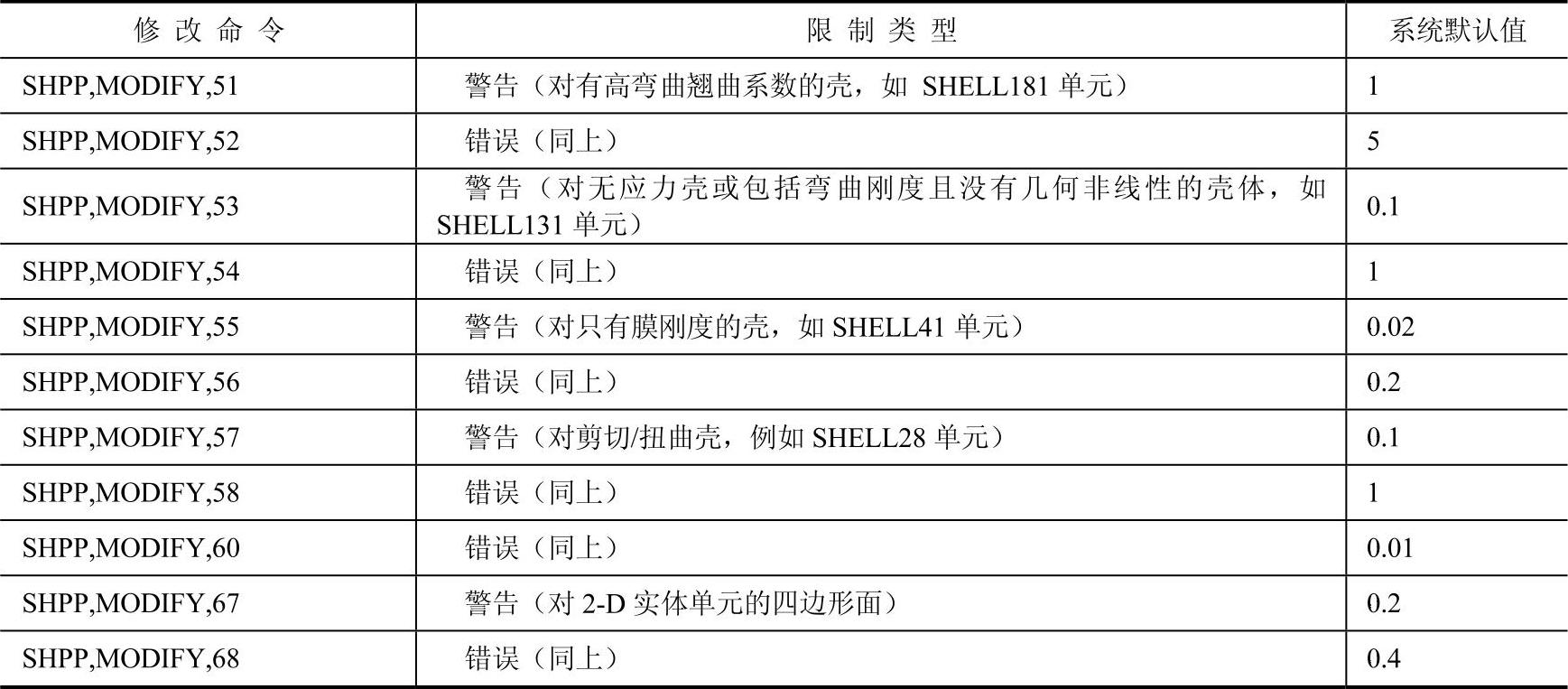
1）将两条对角向量叉乘求出单元平均法向量，图2-13所示为壳单元平均法向量的计算。

2）将单元投影到法向量是在单元平均法向量的平面上计算出投影面积。图2-14所示为壳单元投影到平面上。

3）计算出各顶点到投影平面的距离，在图2-14中，这个距离为2h，各个点到投影平面的距离相等且为h。对于平面四边形，这个距离为0。

4）单元面翘曲系数F_a^w等于边的高度差（2h相邻顶点在平均法向方向的差）除以投影面积的二次方根。

5）除了只有膜刚度的壳单元外的所有的壳单元，如果厚度有效，厚度翘曲系数等于边的高度差除以单元平均厚度，该系数实质上比面积翘曲系数大。

6）达到警告和错误极限翘曲系数（写入警告和错误文件）往往都是面积翘曲系数和厚度翘曲系数（如果有效）中较大的那个。

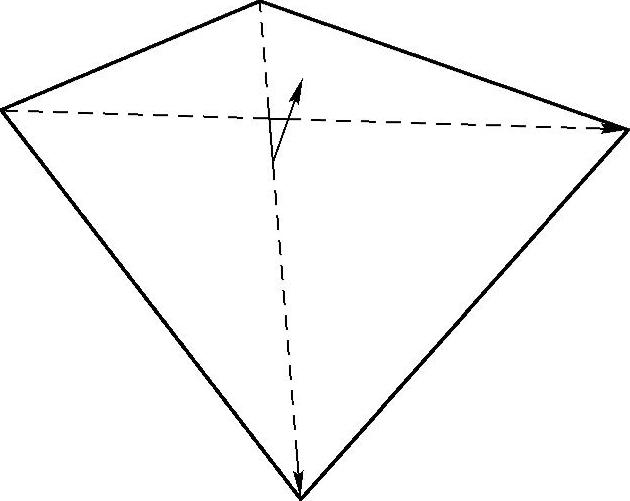
图2-13 壳单元平均法向量的计算

(www.xing528.com)

图2-14 壳单元投影到平面上

7）四边形最理想的翘曲系数是0，即平面四边形。

如图2-15所示，在平面单元上给出翘曲单元，仅移动上面单元右节点，这单元是单位正方形单元，单元厚度为0.1。当上单元的翘曲系数为0.01时，很难与下面的单元区分开。当上单元的翘曲系数为0.04时，开始能区分上下单元。

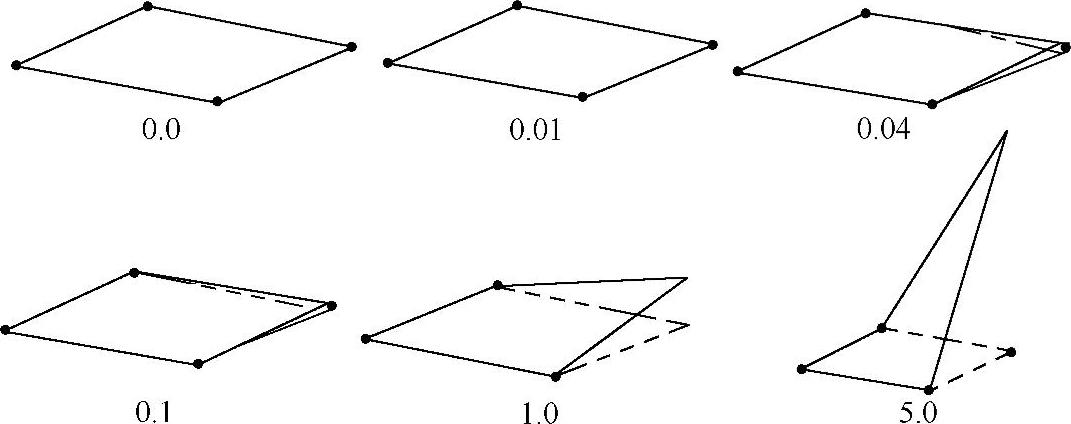
图2-15 翘曲的四边形壳单元

当翘曲系数为0.1时，单元翘曲很明显，但看起来也微不足道。当翘曲系数达到1时，绝大多数的壳单元都会产生错误。

当翘曲系数超过1时，单元会出现明显不能接受的变形。然而，SHELL181单元允许有这么大的变形。此外，翘曲系数最大大约可达到7。用户需要谨慎设置翘曲错误极限值（如果超过默认值5，意味着单元没有真正的翘曲限制）。

2.三维实体单元翘曲系数的计算

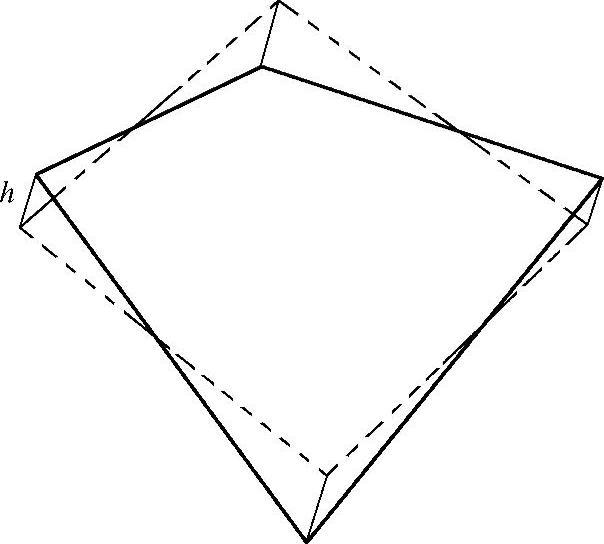
三维实体单元的翘曲系数由表面翘曲系数决定，面的翘曲系数计算过程同四边形壳单元翘曲系数计算中的步骤4。六面体的翘曲系数是6个面中最大的面翘曲系数。四面体的翘曲系数是4个面中最大的面翘曲系数。长方体的翘曲系数为0。图2-16给出了六面体单元的翘曲系数。

图2-16 六面体单元的翘曲系数

底面固定，顶面绕其形心旋转22.5°和45°的翘曲系数分别为0.2和0.4。