VB.NET版：实用计算方法原理与步骤

在高斯消去法的消元过程中，可能出现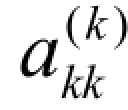 = 0或|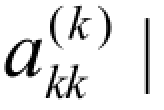|非常小（接近于零）的情况，造成乘数mik=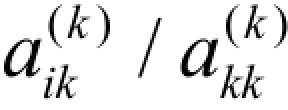溢出，导致消元过程无法进行下去。为了避免这种情况的发生，在第k 次(k = 1, 2, …, n-1)执行高斯消去法之前，从第k 列到第n 列、第k 行到第n 行选取绝对值最大的元素为主元素，通过行、列变换，将其送至主对角线上，此时，乘数的绝对值可保证高斯消去法的顺利进行。

在全主元消去法的消元过程中，列的交换改变了x 分量的次序，因此，在每一次列交换的同时，必须记录调换后的x 分量的排列次序。未知量x1, x2, …, xn 次序调换后记为y1, y2, …, yn，xi 和yi 并非正好一一对应，故应设置一个一维数组专门存储未知量的次序。

采用全主元高斯消去法的算法步骤如下：

步骤1：输入系数矩阵A 和方程组右端向量b 及方程组维数n。

步骤2：对于k = 1, 2, …, n-1，Order[k] = k {一维数组Order 存放解向量元素的序号}。

对于k = 1, 2, …, n-1，执行步骤3 到步骤6。

步骤3：寻找绝对值最大的元素aik jk 及对应的下标ik 和jk，(www.xing528.com)

步骤4：若ik = k，转步骤5；否则，分别交换A 和b 的第k 行和第ik 行对应的元素，

步骤5：若jk = k，转步骤6；否则，交换A 的第k 列和第jk 列对应的元素，同时交换未知量的排列次序，

步骤6：消元计算（参看“2.1.1 算法原理与步骤”）。

步骤7：回代计算（参看“2.1.1 算法原理与步骤”）。

步骤8：对于k = 1, 2, …, n，xOrder[k] = bk。

步骤9：输出原方程组的解x1, x1, …, xn。