【摘要】：高斯消去法的基本思想是设法消去方程组系数矩阵主对角线下方的元素，将其化为等价的上三角矩阵，然后通过回代过程获得原方程的解，即高斯消去法包含消元和回代求解两个过程。其一般求解公式为采用高斯消去法的算法步骤如下：步骤1：输入系数矩阵A 和方程组右端向量b 及方程组维数n。
高斯消去法的基本思想是设法消去方程组系数矩阵主对角线下方的元素，将其化为等价的上三角矩阵，然后通过回代过程获得原方程的解，即高斯消去法包含消元和回代求解两个过程。
1）消元过程
将原方程组Ax =b 记作A( 1)x =b (1)。
第1 步：设x1 的系数
≠ 0，依次用第2 个至第n 个方程中x1 的系数
除以
得乘数
然后将第1 个方程的各系数分别乘以-mi1 并加到第i 个方程对应的系数上，便消去了第i个方程中的x1，得到等价的方程组
或简记为
第k 步(1≤k≤n-1)：设第k-1 步消元已经完成，得到的等价方程组为
或简记为
继续此过程，直至完成第n-1 次消元，得到与原方程组等价的上三角方程组
简记为(www.xing528.com)
2）回代过程
从第n 个方程求出xn，代入第n-1 个方程求出xn-1，直到由第1 个方程求出x1。其一般求解公式为
采用高斯消去法的算法步骤如下：
步骤1：输入系数矩阵A 和方程组右端向量b 及方程组维数n。
步骤2（消元计算）：对于k = 1, 2, 3, …, n-1，若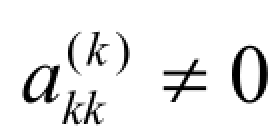
，
步骤3（回代计算）：
步骤4：输出原方程组的解b1, b1, … , bn。
编程时，用右端项数组存储解数组即可，无须另外定义一个解数组。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
