VB.NET版实用计算方法：算法原理与步骤

在牛顿法和牛顿下山法中，需要计算函数y = f(x)的一阶导数，当f(x)的表达式很复杂或 f ′( x) 计算困难时，这两种方法的应用存在不便。割线法（又称弦割法、弦法），是基于牛顿法的一种改进算法，其基本思想是用弦的斜率近似代替目标函数的切线斜率，并用割线与横轴交点的横坐标作为方程根的近似，避免牛顿法和牛顿下山法中函数导数的计算。

经过两点(xk-1,f (xk - 1))和 (x k, f (x k ))的直线方程为L：y =f ( xk )+λ(x -xk-1)，其中λ 为L的斜率，λ=[ f ( xk )-f (xk-1)]/(xk -xk-1)，L 与x 轴交点的横坐标为xk+1= xk-f ( x k)/λ；重复此过程，得x*的近似值序列{xk}。如果序列{xk}收敛，则xk→x*（k→∞）。割线法求解非线性方程f(x) = 0 根的迭代过程如图1.13 所示。

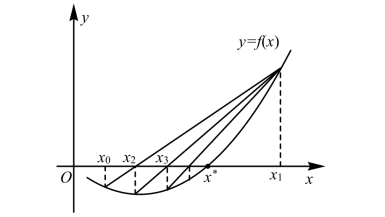
图1.13　割线法求解非线性方程的迭代过程

割线法迭代公式为

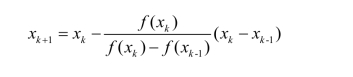
用割线法求解非线性方程f(x) = 0 根的算法步骤如下：(www.xing528.com)

步骤1：输入初始解区间端点x0 和x1、解精度E1 和方程精度E2、最大迭代次数M。

对于K = 1, 2, …, M，执行步骤2、步骤3。

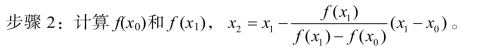
步骤3：若|x2-x1|＜ E1 且| f(x2)|＜E2，输出x2 和f(x2)，计算结束；否则，若f(x0) f(x2)＜0，则x1 = x2，返回到步骤2；若f (x1) f(x2)＜0，则x0 = x2，返回到步骤2。

步骤4：输出“割线法已迭代M 次，没有得到符合要求的解”，停止计算。