实用计算方法算法原理及步骤

将方程f(x) = 0 变形为x = φ(x)，先设法给出根的某个近似估计值x0（迭代初值），令x1 = φ(x0)，并取x1 作为方程根新的近似值，令x2 = φ(x1)，如此反复迭代，就有xk+1 = φ(xk)（k = 0, 1, 2, …），据此，可以得到近似值序列{ xk }。如果序列{ xk }收敛，即xk → x（*k→∞），则x* = φ(x*)。当k 充分大时，有|x k- x *|＜ ε，就可得到满足事先给定精度ε的所求根x*的近似值xk。

求方程x = φ(x)的根就是求曲线y = φ(x)与直线y = x 交点的横坐标x*。迭代求解过程（见图 1.4）：x0→y = φ(x0)(P0 点)→ x1 = φ(x0)→y = φ(x1)(P1 点)→x2 = φ(x1)→y = φ(x2)(P2 点)→…。当φ(x)的变化幅度小于x 的变化幅度时，迭代公式收敛；否则，迭代公式发散。图1.4（a）和1.4（b）为不动点迭代法收敛示意图（xk 不断靠近x*），图1.4（c）和1.4（d）为迭代法发散示意图（xk 不断远离x*）。

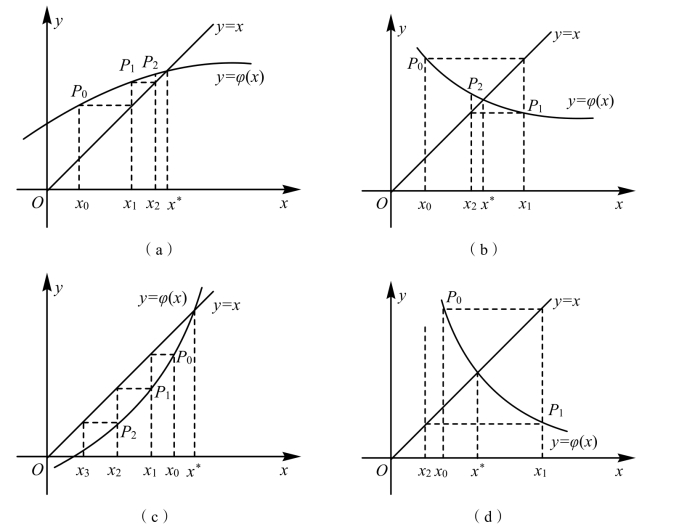
图1.4　不动点迭代法收敛与发散示意图

用不动点迭代法求解非线性方程f(x) = 0 的算法步骤如下：

步骤1：输入迭代初值x0、控制精度E、最大迭代次数M。

步骤2：计算f(x0)，若|f(x0)|＜E，则输出x0，计算结束；否则，往下进行。(www.xing528.com)

对于K = 1, 2, …, M，执行步骤3 至步骤5。

步骤3：计算x1 = φ(x0)。

步骤4：若|x1-x0|＜E 或|x1-f(x1)|＜E，则输出x1，计算结束；否则，往下进行。

步骤5：x0 = x1，返回步骤3。

步骤6：输出“不动点迭代法已迭代M 次，没有得到符合要求的解”，停止计算。