流体力学基础知识-简明运动生物力学

凡是没有固定形状且易于流动的物体就称为流体。人体或器械的运动都是在流体(空气或水)环境中运动的,很多情况下流体(空气或水)对人体或器械运动的影响是不能忽略的。例如,各种球类运动、投掷运动、水中及水上项目的运动等,都会受到流体的作用从而影响其运动的效果。本节从运动生物力学的角度分析人体或器械在流体中的运动,研究如何根据流体的特性、采用合理的动作技术,减小在特定方向上流体的阻力、增大动力。

(一)静止流体内的压强

流体内部任何方向都有压强,在同一深度各个方向的压强都相等。流体内部某一深度的压强等于流体的密度(ρ)、重力加速度(g)、深度(h)三者的乘积,即P=ρgh。

(二)理想流体

流体在流动时各层间有相对滑动,相邻层间存在着摩擦力,称其为内摩擦力或黏滞力。实际上流体是可压缩的。液体压缩较难,气体压缩却很容易,很小的压强差就能导致气体迅速流动。在很多情况下,黏滞性和压缩性对流体的运动影响很小,是次要的因素,而流动性对其影响是主要因素。为了突出流体的这个主要特征,使问题简化,把定常的、无旋的、不可压缩和没有黏滞性的流体称为理想流体。

(三)流体具有流动性和黏滞性

人体的流体运动环境包括空气和水。流体的宏观力学性质是具有易流动性,这是流体区别于固体的属性。在真空状态下,运动的物体受到的阻力及升力为零。物体在流体中运动时,即使做匀速直线运动,物体也会受到流体的阻力。在速度较低的情况下,物体表面会附着一层流体随物体一起运动,从而使物体表面附着的流体层与邻近的流体层之间发生相对运动,由此产生阻碍物体运动的黏滞力,也称为黏滞阻力或摩擦阻力。

(四)流体质点和连续介质模型

流体质点(流体微团)是在研究流体机械运动中所取的最小的流体单元,它的体积无穷小却又包含无数多的流体分子,即微观上充分大、宏观上充分小的分子团。流体质点尺度比分子或分子运动尺度足够大,它可以包含“无数”个分子,而比所研究的力学问题的特征尺度又足够小。

将流体看成连续介质是流体力学研究的基本假设之一。它认为流体是由无数质点(流体微团)组成、质点间没有空隙、连续地充满其所占据的空间的连续体,且质点宏观物理量,如质量m、速度v、压强P、温度T等,各物理量之间可以用连续函数来表示,从而利用数学的方法研究流体的受力情况及运动规律。

(五)流动的分类

①按流体通过空间固定点时,其运动参数是否随时间变化来分类:

a.定常流动:是指在流场中流体中任何一点的运动参数(压力、速度、密度等)不随时间变化的流动,称为“稳态流动”或者“恒定流动”。

b.非定常流动:是指在流场中流体中任何一点的运动参数(压力、速度或密度等任意一个)随时间变化的流动。

②按与空间坐标变量的关系来分类:一维流动、二维流动和三维流动。

(六)流线和迹线

1.流线

流线是在流场中每一点上都与速度矢量相切的曲线(图4-7)。流线是同一时刻不同流体质点所组成的曲线,它是该时刻不同流体质点的速度方向。

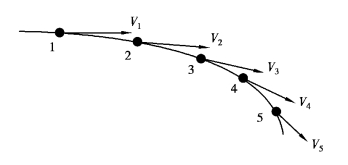
图4-7　流线

2.流线的性质

①在运动流体的整个空间,可绘出一系列的流线,称为流线簇。流线簇的疏密程度反映了该时刻流场中速度的不同。

②当为非定常流时,流线的形状随时间改变;当为定常流动时,流线的形状和位置不随时间而变化。

③一般情况下,流线不能相交,不能折转,只能是一条光滑曲线。

3.迹线

迹线是流体质点在空间运动时所描绘出来的曲线,即流体质点运动的轨迹。

4.迹线的特点

①迹线的切线给出的是同一流体质点在不同时刻的速度方向。

②迹线是单个质点在连续时间过程内的流动轨迹线。

③迹线只与流体质点有关,对不同的质点,迹线的形状可能不同。但对某一确定的质点而言,其迹线的形状不随时间变化。

(七)流管和流束

在运动流体空间内垂直于流动方向作一微小的闭合曲线,通过该闭合曲线上各点的流线围成的细管称为流管(图4-8)。由于通常情况下流线不会相交,因此,流管内、外的流体都不会穿越管壁。

图4-8　流管和流束

在各个时刻,液体质点只能在流管内部或沿流管表面流动,而不能穿越流管。流线组成了流束,流束是流管内的流线簇。流管仿佛就是一根虚拟的水管,其周界可以视为虚拟的固壁。在日常生活中,自来水管的内表面没有流体的穿透,这一点与流管是相同的。但在自来水管的内表面上,流体被黏附导致速度为零,而流管壁并没有这种约束,两者之间还是有一定的区别。

(八)层流和湍流

层流和湍流是流体的一种流动状态。当流速很小时,它做层状的流动,流体分层流动,互不混合,称为层流,也称为稳流或片流[图4-9(a)];逐渐增加流速,流体的流线开始出现波浪状的摆动,摆动的频率及振幅随流速的增加而增加,此种流况称为过渡流;当流速增加到很大时,流线不再清楚可辨,流场中有许多小漩涡,层流被破坏,相邻流层间不但有滑动,还有混合。这时的流体做不规则运动,有垂直于流管轴线方向的分速度产生,这种运动称为湍流,又称为乱流、扰流或紊流[图4-9(b)]。

图4-9　层流和湍流

(九)过流断面和流量

1.过流断面

某一研究时刻的流管或流束一个横断面,称过流断面。过流断面是与流管内所有流线正交的横断面,不一定是平面,其形状与流线的分布情况有关,只有当流线相互平行时,过流断面才为平面,否则为曲面。过流断面用S表示。(www.xing528.com)

2.流量

流量是指单位时间内通过流管或流束中过流断面的流体量,用Q表示,Q=vS,其中v是流体的平均速度。流量的度量单位一般用体积,也可以用质量或重量。

(十)流体的连续性原理——连续性方程

这是描述流体流速与截面关系的定理。当流体连续不断而稳定地流过一个粗细不等的流管时,流管中任何一部分的流体都不能中断或挤压起来,在同一时间内,流进任意过流断面的流体质量和从另一过流断面流出的流体质量应该相等。即

ρ1v1S1=ρ2v2S2=常数

这就是流体运动的连续性方程式。如果是不可压缩流体,则ρ保持不变。连续性方程式即为

v1S1=v2S2=常数

可以得到结论:流束的平均流速与过流断面的面积成反比。即在流量一定的情况下,流束断面大则流速小,流束断面小则流速大。

(十一)流体的能量守恒原理——伯努利方程

利用功能原理(外力所做的总功等于机械能的增量)可以推导出理想液体做定常流动时的压强P、速度v和高度h之间的关系。

假设流体在重力场中做定常流动,全取一段细流管作为研究(图4-10)。由于流管取得非常小,可以认为在同一个过流断面截面上的每一点的流体的流速和压强都是相同的。设在左端,其截面积为S1、速度为v1、压强为p1、距离参考面的高度为h1;在右端,截面积为S2、速度为v2、压强为p2、距离参考面的高度为h2。S1-S2这段流体在极短的时间Δt(Δt=t2-t1)内从S1-S2位置移动到S′1-S′2位置,讨论在Δt时间内各种力对这段流体所做的功及由此引起的能量的变化。

图4-10　伯努利方程的推导

1.压力所做的功

理想流体在流动时没有黏滞性;流管外侧面的流体对这段流体的压力方向垂直于流管表面,这个压力不做功;只有流管两端的流体对管内的流体压力才做功。由于Δt时间很短,从S1处到S′1处以及从S2处到S′2处的流体的压强、流速及流管的过流断面截面积、高度的变化都是很微小的。

作用在S1处的压力F1=p1S1为推力,所做的功为正功,即

A1=F1d1=F1v1Δt=p1S1v1Δt

作用在S2处的压力F2=p2S2为阻力,所做的功为负功,即

A2=F2d2=F2v2Δt=p2S2v2Δt

在时间Δt内外力所做的净功为

A=A1-A2=p1S1v1Δt-p2S2v2Δt

式中,S1v1Δt和S2v2Δt分别等于包围在S1S′1和S2S′2之间的流体的体积。按流体连续性原理,它们是相等的,用体积V表示,且这两部分流体的质量也是相等的,以m表示流体的这一质量,则上式可写成

A=p1V-p2V

2.重力势能的增量

W=W2-W1=mgh2-mgh1

3.动能的增量

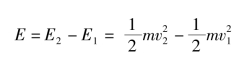
根据功能原理有

A=W+E

即

因流体段是任意选取的,故

式(4-1)是瑞士科学家伯努利于1738年首先导出来的,称为伯努利方程。方程式中pV具有能量的量纲,可把它看作体积为V的流体处于压强p之下所具有的能量,称为压强能。伯努利方程可叙述为:在重力作用下一定质量的理想流体做定常流动时,在流管的任一过流断面处,其动能、势能、压强能之和为一常量。将式(4-1)两边同时除以V,得

式中,是流体的密度。式(4-2)是伯努利方程常用的表达式。该式说明,理想流体做定常流动时,在同一流管的任一过流断面处,单位体积流体的动能、势能、压强能之和是一个常量。一般地,对不同的流管,这个常量的值是不同的。伯努利方程是流体力学的基本定律之一。

伯努利方程是人体或器械在流体中进行技术分析的主要理论基础。假如流体在水平流管中流动时,即流体的高度不发生变化的情况下,伯努利方程可简化为

由式(4-3)可知,在同一水平管中流动的流体,流速小的地方压强大,流速大的地方压强小。

由连续性方程及伯努利方程,可以得出重要结论:理想液体在水平管中做定常流动时,压强和流速的关系为截面积大,则流速小,压强大;截面积小,则流速大,压强小。