抛体运动的力学分析基础是运动的独立性原理或运动的叠加原理,是指一个运动可以看成几个各自独立进行的运动叠加而成,即任何一个方向的运动都不会因为另外一个方向的运动是否存在而受到影响。在分析抛体运动时,一般采用直角坐标系,从竖直方向和水平方向去研究。
(一)抛点与落点在同一水平面上的斜抛运动
如图4-3所示建立直角坐标系,根据运动的独立性原理,斜上抛运动可以看作水平方向的匀速运动和竖直上抛运动。运动开始时,抛射体具备一定的初速度v0,并与水平面成抛射角α,则抛射体在水平方向和竖直方向上的初速度分量分别为
图4-3 同一水平面上的斜抛运动
如果不计空气阻力、风向及风速的影响。设抛出的初始时刻为0,可得到抛射体在初始时刻的水平速度与竖直速度分别为
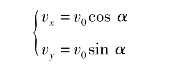
运动到t时刻的位置为
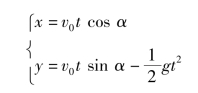
抛射体达到最大高度的时间为
抛射体达到的最大高度为
从抛出点到落地点的腾空时间为
抛射体飞行的远度为
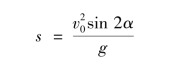(www.xing528.com)
从理论上计算当α=45°时飞行的距离最远。
(二)抛点高于落点的斜抛运动
如图4-4所示,以掷铅球为例,设出手点的高度为h,出手初速度为v0,抛射角为α,投掷远度为S。
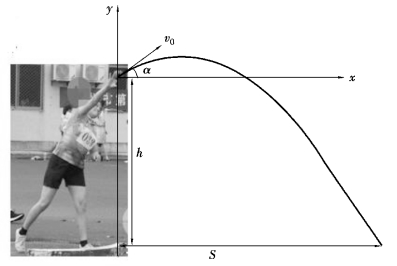
图4-4 抛点高于落点的抛体运动
设铅球从投出到落地的总时间t为,则
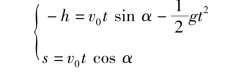
-h表示落点在原点以下。解得时间t为
最终得到投掷的远度公式为
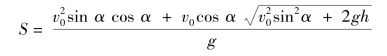
(三)抛点低于落点的斜抛运动
篮球投篮时球的出手点低于球的落点,投篮时,落点的速度方向直接影响着投篮的命中率(图4-5)。计算结果表明,运动员在出手点高度一定时,初速度与抛射角的配合只有在阴影区(图4-6)才有机会投中空心球,这对篮球的定点投篮训练有一定的帮助。
图4-5 抛点低于落点的抛体运动
图4-6 投篮时初速度与抛射角之间的关系
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
