不平等性测度指数与社会福利：一项研究成果

经济学家发现，不平等的程度越高，不平等所导致的社会福利损失就越大。对不平等指标中隐含的社会福利函数的考察表明，有些指标具有不可接受的特征，也不能表达社会福利含义。因此，对不平等指标的选择，除了从公认的5个公理方面判断之外，还需要从不平等指数的社会福利含义来进行判断。要判断不平等指标是否具有社会福利含义，需要确定不平等指标与社会福利函数之间的关系。下面从社会福利含义方面判断基尼系数与泰尔指数是否具有可接受的特征。

1.社会福利函数

福利经济学家通过构建一个次序规则对社会的所有状态进行排序，此次序规则通常依据的是某个社会福利函数（social welfare function），即依据某个社会福利函数测度各种状态下的社会福利并进行排序。早期社会福利函数主要采用效用函数形式，设消费分布X=（x1，x2，…，xn），个体i（收入为xi）的效用为μi（xi），那么整个社会的福利函数为：

此公式表明效用主义的社会福利函数是可加可分离的。一般要求效用函数μi（xi）为递增的凹函数，至于每个人的效用函数是否相同，对最终结果有很大影响。如果每个人的效用函数相同，则可以证明在总收入一定的条件下，最大化社会福利的结果是平均分配；而如果每个人的效用函数不同，最大化社会福利函数的结果可能是一个高度不平均分配。社会福利函数未必就是效用主义的，为了更一般地解释社会福利函数，柏格森和萨缪尔森提出了广义社会福利函数的概念（Bergson，1938；Samuelson，1947）。公式为：

阿罗将社会福利定义为群体决策的某个规则（Arrow，1951）。道尔顿最早使用社会福利的损失来测度不平等。他选择的社会福利函数为严格凹函数，即当平均分配的社会总效用为W（μ·en），其中en表示元素全为1的n维行向量（Dalton，1920）。则，道尔顿不平等指标为：

经过很长一段时间，学者才关注道尔顿指标。Atkinson认为道尔顿指标并不满足仿射变换不变性，并推导出了一个合适效用函数后给出的不平等指标：

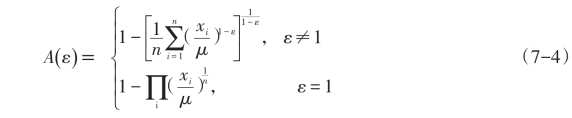
基于社会福利函数基础上的不平等指标，目前普遍采用Atkinson提出的平均分配的同等收入（equally distributed equivalent income，EDEI）的概念（Atkinson，1970）。平均分配等值收入的含义是，当每个人均取得平均分配的同等收入时，该状态的社会福利与实际收入分布的社会福利是相等的。设EDEI为ξ，也就是W（ξ·en）=W（X），从而不平等指标为：

这样比较不同收入分布的不平等程度，就等价于比较相应的EDEI与μ的比值，即对比相应的社会福利函数。判断不平等指标的好坏，一定程度上可以通过比较社会福利函数的优劣来判断。当然有些不平等指标不能表示为社会福利函数的形式，因此也不能作为一个好的指标来度量不平等。

2.基尼系数的社会福利函数

基尼系数不仅可以用来度量收入的不平等，同时还可以度量消费的不平等、财富的不平等和任何其他事物分布的不均状况（徐宽，2003）。但基尼系数用来度量收入的不平等最为普遍。因此这里以基尼系数为代表研究不平等指标的社会福利含义。基尼系数最初是作为一个表达分布不均等的指标提出的。在很长一段时间内，人们只是把它和方差或标准差当成作用类似的分布不均等的指标。当学者必须从中选择一个指标，就会发现：若不考察这些指标的社会福利含义，就很难判断哪个指标比其他的指标更为合适。因此，学者们便开始考察各种不平等指标和社会福利函数之间的关系。现在经济学家已经发现许多不平等指标与社会福利函数之间存在直接但又不是一目了然的关系。这些发现还表明，不平等的程度越高，不平等所导致的社会福利损失就越大。这些理论的发现使基尼系数的社会福利含义更为清晰。(www.xing528.com)

从统计学的角度来看，基尼系数是基尼平均差的函数，它最早用来度量一个分布的离散程度。现在仍可用于此目的。道尔顿在1920年提出了一个评价社会不平等指标的起码的标准“庇古—道尔顿转移支付原理”。在阐述这一原理时，道尔顿写道：“我们首先要阐述转移支付原理：如果这个社会中只存在两个人，那么如果财富从富者转移到穷者，不平等程度就会降低。但是这里有一个限制条件，就是富者的财富转移不能太大，以至于使穷者和富者的经济地位互换，并使新的穷者更穷，新的富者更富。这种转移支付的量的极限是使两者完全平等。”我们可以进一步地说，不管这个社会中存在多少人，也不管他们的财富是多少，如果在任何两个人之间做如上的转移支付，那么整个社会的不平等就会减少（Dalton，1920）。道尔顿还注意到，基尼系数仅仅是基尼相对平均差的二分之一。道尔顿认为，因为相对平均差符合上述的转移支付原理，所以基尼系数也符合上述的转移支付原理。因此，认为基尼系数是一个可行的度量不平等的指标。

研究不平等和社会福利的损失之间的规范经济学方法出现比较晚。Kolm（1969）倡导用社会福利函数去度量收入不平等。Atkinson（1970）认为，如果要选择一个恰当的度量不平等的指标，考虑其社会福利的含义是非常重要的。Atkinson说：“首先，仅使用不平等指标会使人忽视以下事实，如果不知道社会福利函数的形式，就不可能对分布给出完全的优劣排序。其次，对不平等的指标中隐含的社会福利函数的考察表明，有些指标具有不可接受的特征，也不能表达社会福利含义。由于上面两个原因，我们应该拒绝那些常用的不平等的度量方法，接受那些具有社会福利函数特征的指标。”（Atkinson，1970）

将基尼系数和社会福利函数联系起来的途径是将基尼系数用平均分配的同等收入（EDEI）来定义，或是用Atkinson（1970）、kolm（1969）和Sen（1973）所提出的代表性收入来定义。运用这种方法，度量收入不平等的指标I可以表示为平均分配的同等收入的值ξ和平均收入的μ的函数，见公式（7-5）。

如果I是定义在社会福利函数之上的基尼系数，那么I就可以用IG或是G来表示。根据这个公式，如果平均分配的同等收入的值ξ等于μ，那么I等于0，这就表明社会中不存在不平等。如果平均分配的同等收入的值ξ小于μ（例如，前者是后者的70%），那么I将会大于0，小于1（这时，I值将是0.3），这就表明存在一定程度的收入不平等。当然，如何计算平均分配的同等收入的值ξ是极为重要的。一般说来，平均分配的同等收入的值ξ是这样决定的，对于给定一个特定的社会福利函数，平均分配的同等收入的值ξ是一个收入水平，当社会每个人都得到它时，全社会所获得的社会福利函数值与实际不平均的收入分布所产生的社会福利函数值相等。

图7-4给出了两个人的收入分布，也就是y点（第一个人的收入为y1=2，第二个人的收入为y2=5）。图中，45度直线代表收入完全平等，两个人的收入一样，即y1=y2。I1和I2为社会福利函数的无差异曲线。由于实际收入分布y出现在无差异曲线I2上，而且无差异曲线I2和45度直线有一个交点，即平均分配的同等收入（EDEI），这个交点所代表的社会福利水平和y所代表的社会福利水平相当。因此，对于给定的社会福利函数，实际收入分布y所代表的社会福利水平和平均分配的同等收入（EDEI）所代表的社会福利水平没有什么不同（徐宽，2003）。

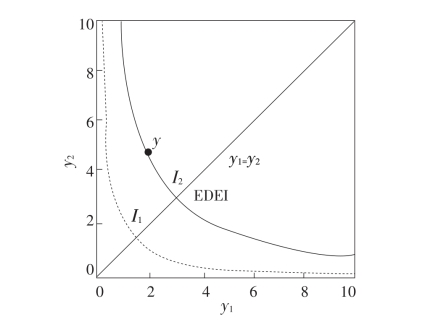
图7-4　社会福利函数和EDEI（徐宽，2003）

基尼系数就可以通过与基尼社会福利函数相联系的平均分配的同等收入（EDEI）来计算：

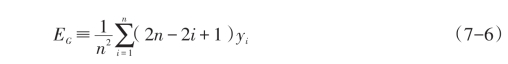
这个平均分配的同等收入（EDEI）产生于基尼社会福利函数这个基尼福利函数对贫穷者赋予了较大的权重，对于富裕者赋予了较小的权重。权重是由收入排序的序数而不是收入多少本身决定的。基尼系数就可以定义为平均分配的同等收入（EDEI）和平均收入的函数：

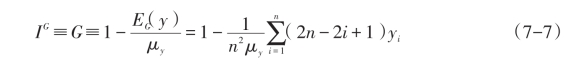
由于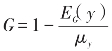的取值位于0（表示完全的平等）和1（表示完全的不平等）之间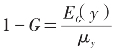，也位于0（表示完全的平等）和1（表示完全的不平等）之间。所以，1-G可用以度量收入的平等程度。

上述公式清楚地表明基尼系数的社会福利含义。如果基尼系数为0.3，这表明，不平等将社会福利水平降到现有的社会总收入平均分配后所能达到的社会福利水平的70%。如果把现有的社会总收入平均分配，那么不平等将会降为0，这也说明，在对厌恶不平等的社会里，基尼系数低的收入分布给社会所带来的社会福利比基尼系数高的收入分布所带来的要高。同样地，通过分析，泰尔指数也具有一定的社会福利含义。

因此，基尼系数与泰尔指数在不平等度量中被认为是相对比较好的度量指标。