令n≥2，倒立金字塔图RP（n）是n层的由三角形堆砌而成的图形，就像一个倒过来的金字塔。
RP（2）
RP（2）有1+3＝4个小三角形，RP（3）有1+3+5＝9个小三角形，一般RP（n）有1+3+5+…+（2n－1）＝n2个小三角形。
RP（3）
我们现在来玩这个游戏，先从最小的RP（2）开始，在最左上角的三角形写上［0］3，然后依次由左向右
用以下的运算填写邻边的三角形，一层填完后，就接下来填下一层，由上面
的三角形的数填下层的小三角形，你会看到
好，现在你试试RP（3）的填法。”
小王子很快得到以下填法：
然后他试RP（4）：
接下来他试试RP（5）：
他再试RP（6）：
“小王子，你看到什么奥妙的地方吗？”
“我看到从上到下的斜对角线如果第一个三角形是0，底下会按照0，1，2，0，1，2的循环节一直下去。”
“对，你的观察正确，如果不是0会是怎样呢？”
“如果开头是1，就会有1，2，0，1，2，0的循环节；开头是2就会有2，0，1，2，0，1的循环节。”
“你要不要对2的情形验证一下？”
“好的，老爷爷。”
RP（2）
RP（3）
RP（4）
RP（5）
“老爷爷，真的是这样。”
“好，现在我们要用另外的规定。”
“老爷爷，这是什么东西？”
“它是叫等幂群胚。”
我要画它的游戏规则：
“为什么叫‘等幂群胚’呢？”
“因为它满足这样的‘等幂律’，即：
x◦x＝x
你看它的乘法表的对角线呈现：［0］3◦［0］3＝［0］3
［1］3◦［1］3＝［1］3
［2］3◦［2］3＝［2］3”
“以后有机会我会再深入讲这个代数系统的一些有趣性质，现在我要用这群胚来玩一种游戏。
先看◦［0］3规则。
［情况1］
好，你现在从这金字塔图的最左上角的小三角形填上0，你看最后整个图会有什么情况？”
小王子很快对RP（2）、RP（3）及RP（4）填好数。
RP（2）
RP（3）
RP（4）
“我得到所有的RP（n）的小三角形都是0！”(www.xing528.com)
“你现在用1填在金字塔图上的最左上角的小三角形，看有什么变化？”
小王子给出了以下RP（2）、RP（3）及RP（4）的3个结果。
RP（2）有0个
，3个
，1个
RP（3）有0个
，6个
，3个
RP（4）有0个
，10个
，6个
“小王子，你能看出这里有什么美妙的现象吗？”
经过25分钟的观察和计算，小王子给出以下答案。
“老爷爷，我想我有这样的结果：
［定理1］对于n≥2，如果在最左上角先填上1，情况1的涂色会有这样的结果：
RP（n）有0个
我们有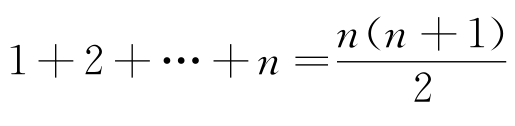
个
至于
的个数，可以用
的计算得到。
是不是这样？”
“小王子，你做得很好，的确是像你所说的那样。
现在你是否可以对最左上角的小三角形填上2，然后看有什么结果？”
小王子这次用不到10分钟的时间，迅速地得到这样的定理。
［定理2］对于n≥2，如果在最左上角先填上2，情况1的涂色会有
小三角形有0个，
小三角形有
个，
小三角形有
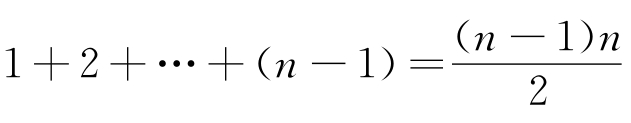个，
这是他画出的图：
“孩子，你可以再试试情形2和情形3的情形。”
情形2
情形3
“老爷爷，我有类似的定理：
［定理3］对于n≥2，情况2的RP（n）会有这样的结果：
（a）最左上角填上0，
有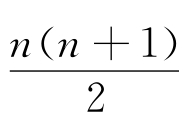
个0三角形，0个1三角形及
个2三角形；
（b）最左上角填上1，
有0个0三角形，n2个1三角形及0个2三角形；
（c）最左上角填上2，
有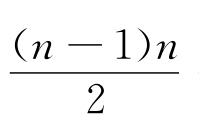
个0三角形，0个1三角形及
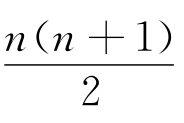个2三角形。
［定理4］对于n≥3，情况3的RP（n）会有这样的结果：
（a）最左上角填上0，
有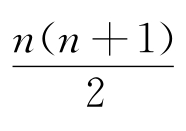
个0三角形，
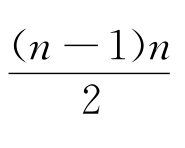个1三角形及0个2三角形；
（b）最左上角填上1，
有
个0三角形，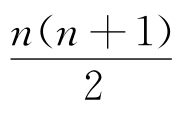
个1三角形及0个2三角形；
（c）最左上角填上2，
有0个0三角形，0个1三角形及n2个2三角形。”
“很好，你现在是知道怎样玩这种游戏了。”
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
