eCognition软件中的面向对象分类方法可以分为阈值法分类、隶属度分类、最近邻分类、分类器分类4大类。
4.2.3.1 阈值法分类
阈值法分类是图像分类里的一种软分类，其原理是根据各种特征的分布来得到阈值，这是一种“真”和“假”的逻辑判定。符合这一阈值条件的对象，则将其完全归为某类，否则就归为其他类。阈值分类法的关键在于找到某地物的分类特征，并统计该特征的分布情况，定义该特征下的阈值条件（郑云云，2015）。
4.2.3.2 隶属度分类
隶属度分类是一种基于规则模式的模糊分类方法，经分割后的影像对象不是被硬性地分为某一类，而是在某种程度上属于某类，同时在另一种程度上属于另一类（刘陈立等，2017）。对象与类之间的关系不是确定的，而是通过隶属度函数表达。隶属度函数是一个模糊表达式，通过将影像对象的任意特征值转换为0～1之间的数值，表示该对象属于某类地物的可能性，隶属度函数的值越大，则该对象属于此类的可能性就越大（李中夫，1987）。单一的隶属度函数表现为一条二维曲线，横坐标为类别的特征值，纵坐标为类别的隶属度，在特征值与隶属度间建立了直观的联系。常用的隶属度函数有二值函数、正态分布函数、阶跃函数、S型函数等，在信息提取过程中选择一种最适合的函数描述分类特征。eCognition中的预定义函数如图4-12所示。
图4-12 预定义隶属度函数
隶属度函数的确定方法有三种：一是根据个人经验或主观认识给出隶属度的具体数值；二是根据问题的性质选用一些典型的函数作为隶属度函数；三是根据模糊统计来确定，通过心理测量来进行，研究的是事物本身的模糊性。
4.2.3.3 最近邻分类
最近邻（NearestNeighbor）分类的原理：对选择的样本进行样本类特征的统计，然后以统计出的特征向量为中心，对待分类的对象中包含且用于分类的特征同样本类特征求“差”值作为距离，把对象距离最近的那个样本类作为对象类别归属（陈金丽，2009）。假设有m个类别，每个类别有N个样本，待分类影像对象o与样本对象s之间的特征值距离d计算公式为：
式中，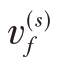
表示样本对象s的f对象特征值；
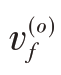表示待分影像对象o的f对象特征值；σf为f对象特征的标准差。该方法操作直观、简单，处理速度快，但是不能很好地运用上下文关系。
4.2.3.4 分类器分类
eCognition中的分类器有贝叶斯分类器、K最近邻分类器、支持向量机分类器、决策树分类器和随机森林分类器。
1.贝叶斯（Bayes）
贝叶斯是一种基于贝叶斯定理带有强独立性假设的简单概率分类器，由Good等（1965）于1966年提出。贝叶斯分类器只需要少量的训练样本数据去评估分类所必需的参数（变量的均值与方差）（董立岩等，2007）。贝叶斯定理指的是已知事件B发生的情况下，事件A发生的概率，即P（A|B）已知；以此求出事件A发生情况下，事件B发生的概率P（B|A）。公式为：
贝叶斯分类的定义：设有待分类项x=
以及类别集合
，其中ai(i=1，2，…，m)表示x的每个特征属性。各类别的条件概率P(yk|x)=
（Zhang etal，2009）。
2.K最近邻（K NearestNeighbor，KNN）
K最近邻由Cover等（2009）于1968年提出，该算法的主要思想为：当一个未知类别样本在特征空间中最近邻（或最相似）的k个样本均属于同一类别时，则该样本也属于该类。通常基于距离来衡量待分类样本与训练样本（近邻样本）之间的相似度，如欧氏距离、曼哈顿距离、闵可夫斯基距离等。KNN算法简单高效，无参数化，分类效果好，鲁棒性强，常被用于文本分类、图像分类以及模式识别等领域。KNN算法的分类步骤如下：
第一步，确定K的值，并计算待分类样本X与训练样本T之间的距离，假定每个样本包含n个特征，则训练样本与待分类样本的特征向量可表示为T=(t1，t2，…，tn)和X=(x1，x2，…，xn)，二者之间的距离D(T，X)的计算公式为：
第二步，根据D(T，X)对所有训练样本按照由大到小的顺序进行排序，并从中选取排在前K位的训练样本。(www.xing528.com)
第三步，确定以上训练样本各自所属的类别，并统计每个类别出现的频率，将其中出现频率最高的类别作为样本X的类别。
3.支持向量机（SupportVectorMachine，SVM）
SVM由Cortes等（1995）提出，该算法寻找模型复杂度与学习能力之间的最佳折中，以期获取较高的泛化性能。该算法的优点是适合解决小样本问题，可避免当训练样本个数与高维特征相比相对较少时，分类精度下降的现象。
SVM算法的原理：给定一组训练样本，每个样本类别已知，SVM通过已知样本建立模型，通过模型找到最优的线性分离超平面，从而对样本类别进行判断（范昕炜，2003）。在SVM中用核函数将非线性可分离类别从原始特征空间映射到高维空间，从而在高维空间中找到线性超平面进行分类。运用最大边缘概念，即使得超平面和与其最近的特征向量的间隔最大化，以此来找到类别间的最优分离超平面，特征向量被称为支持向量。常用的核函数如下：
线性核函数：K(xi，xj)=(xi，xj)；
多项式核函数：K(xi，xj)=[(xi，xj)+1]q；
Sigmoid核函数：K(xi，xj)=tanh [γ(xi·xj)+d]；
径向基（Radial Basis Fu nction，RBF）核函数：K(xi，xj)=exp(-γ|xi-xj|2)。
式中，q、d和γ表示核函数参数，通常基于人工经验或交叉验证方法获取。
4.决策树（Decision Tree，DT）
决策树方法最早由Breiman等于1984年提出，是一种典型的用于数据挖掘的非参数方法（Breiman etal，1984）。eCognition软件自带的决策树算法为分类回归树（Classification and Regression Tree，CART）算法。分类回归树是一种二叉树，每个节点按照某个属性分为2个子节点，当各个节点所包含的类别相同时，节点停止划分，此时的节点称为叶子节点（于文婧等，2016）。分类回归树的构建包括以下步骤：
第一步，创建根节点，其中包括所有的待分类的样本；
第二步，按照样本所具有的属性进行划分，然后计算每个划分产生的GINI impurity（GINI不纯度指标，指的是样本在按照某个属性划分后被选中的概率与其被分错的概率的乘积），以该值最小作为划分依据，由此生成子节点；
第三步，对第二步生成的子节点再次按照GINI指标进行划分，直至所有节点中的样本类别一致或者只有一个样本，此时所形成的节点为叶节点；
第四步，对所生成的树进行剪枝，剪枝的目的是防止噪声数据的过拟合现象。
5.随机森林（Random Forest，RF）
RF由Breiman（2001）提出，包含多个决策树，输出类别由每个决策树分出的类别来决定。随机森林的构建过程为：
（1）随机从训练样本N中有放回地抽取n个样本，作为决策树的输入样本；
（2）从M个样本特征中随机选取m个特征，作为每个结点的输入样本特征，其中m远小于M；
（3）以m个特征的最优分裂作为该结点的分裂规则；
（4）每棵决策树均最大限度地生长，不剪枝（尚明，2018；郭玉宝等，2016）。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
