复数的四种表示方法及代数式转化

复数有四种表示方法，如果遇到复数的加、减法运算，需要将复数的另外三种形式转化为代数式后进行加、减法运算.对于三角式r（cosθ＋isinθ）、指数式reiθ、极坐标式都需要确定模r和辐角主值θ，将r和θ代入三角形式r（cosθ＋isinθ）中化简后，可以得到复数的代数式.

【例2－28】　将下列复数的极坐标式化为代数式：

解

注：可以用手机计算器求解.

通常情况下，正弦量可以化为平面内的旋转的复向量（相量），复向量的形式是复数的极坐标式，因此也能化为代数式.

【例2－29】　求正弦量i＝10sin（2t＋50°）A的相量极坐标式并转化为代数式.

解　最大值是10 A，

相量（极坐标式）表示：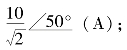

相量（代数式）表示：

同样，知道模和辐角主值及角频率ω，逆向思考也可以将相量化为正弦量.

✧任务解决

解　先将两个正弦电流i1＝70.7sin（314t－30°）（A），i2＝60sin（314t＋60°）（A）化为相量的形式：

由于要计算复数的加法i1＋i2，故需要将的极坐标式转化成代数式.

i＝i1＋i2＝（43.3－j25）＋（21.2＋j36.8）＝64.5＋j11.8.

将i还原回正弦量，故需要将代数式转化成极坐标式.

i＝64.5＋j11.8，因为a＝64.5，b＝11.8所以，复数在第一象限，故辐角主值

将和电流还原成正弦量为

✧能力训练

求两电压之和u1＋u2（注：两电压的ω值相等才能相加）.

✧评估与测试(www.xing528.com)

1.已知正弦量50sin（30t－10°）.

（1）写出其三要素和有效值；

（2）画出相量图，求模r和辐角主值θ；

（3）写出最大值相量和有效值相量.

2.z1＝3＋4i，z2＝－8i，计算z1＋z2.

3.在复平面内画出下列复数图像，并计算模和辐角主值：

4.将下列复数的代数式转化成三角式、指数式和极坐标式：

5.将下列复数的指数式化为代数式：

6.已知，计算z1＋z2.

7.将3＋4i化为角频率为314 rad／s的正弦量.

8.将正弦量180sin（314t＋30°）化为代数式.

✧拓展阅读

爱迪生和特斯拉

爱迪生是一个万人敬仰的伟大发明家，他一生的发明超过2000个，其中申请专利的就有1000多项，是真正的发明之王.然而，他曾经和交流电的发明者尼古拉·特斯拉有一场电流之争.

1882年，爱迪生发明的白炽灯彻底获得市场认可后，爱迪生所创办的电气公司（现通用电气公司的前身）开始建立电力网，输送直流电.不久之后，曾在爱迪生公司工作过的尼古拉·特斯拉发明了交流电，最终这项技术被威斯汀豪斯电气公司买下，成为爱迪生直流电网最大的竞争对手.

最初，威斯汀豪斯电气公司想以交流电这项技术和爱迪生合作，但爱迪生受限于本身自大的心态和自己在直流电方面的投资利益，不愿意承认交流电的使用价值，固执地站在交流电的对立面，以自己的影响力大力宣传“交流电不如直流电”这一说法.爱迪生耍了很多手段与尼古拉·特斯拉所发明的交流电展开了战争，最后以惨败告终.

直流电由于具有不利于长途送电等缺点，成本很高，如每隔1 km就要增设发电站，但交流电却可用变压器变压来长途输电.交流电比直流电在很多方面更具优越性，因此它被用于绝大多数的领域，生活中插座里的电就是交流电.

这个故事告诉我们，任何事物都有其优、缺点，应发挥事物的优点为人类服务，而避开其缺点.