Agent i在与邻居节点Agent j进行观点交互时会获得个体间交互收益Uf。一方面，个体i与熟悉的人进行交互时得到的收益值高于与陌生人交互得到的收益值；另一方面，个体与意见相似者进行交互所得的收益也会高于与意见相背者交互得到的收益。基于此，两个个体进行观点交互得到的收益与他们之间的亲密度hij及友善度gij有关，具体如图7-4及公式（7-6）—公式（7-8）所示。
其中亲密度hij及友善度gij的详细计算过程如下文所示。
（1）亲密度hij
亲密度表示网络中部分个体的相互连接关系的情况。图7-4中，人形节点表示网络中进行交互的个体，连边表示个体间的连接关系。
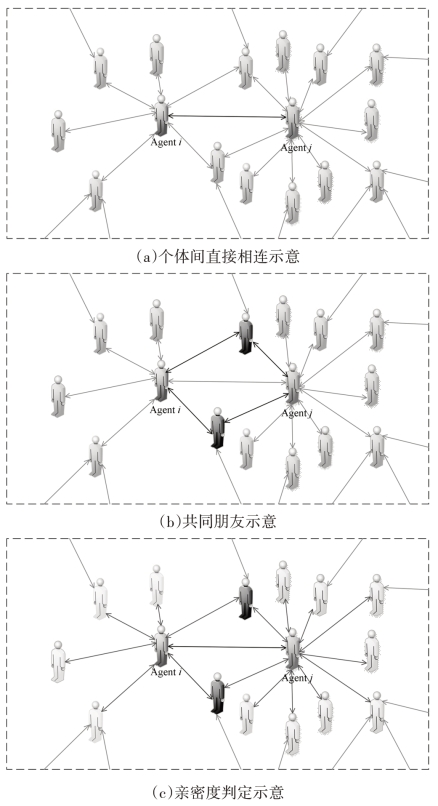
图7-4 亲密度hij计算示意图(www.xing528.com)
如图7-4（a）所示，Agent i与Agent j直接相连［如图7-4（a）中的黑色连线所示］，说明他们之间存在交互关系。如图7-4（b）所示，所有与Agent i与Agent j相连的个体中，有两个共同的相连个体［如图7-4（b）中的灰色人形节点及黑色连线所示］，说明这两个个体同时与Agent i和Agent j存在交互关系，即这两个个体是Agent i与Agent j的共同朋友。在复杂网络中经常会出现“朋友的朋友就是你的朋友”的现象，而共同朋友多的两个个体之间的亲密度往往会高于共同朋友少的两个个体之间的亲密度。因此，本章假设两个个体之间的亲密度大小与共同朋友的数量成正相关关系。然而如图7-4（c）所示，由于与Agent j相连接的个体数量远大于与Agent i相连接的个体数量，因此，尽管i，j之间的共同朋友数量相同，但是Agent i与Agent j对彼此的亲密度判定结果不同。假设网络中所有与Agent i相连接的个体数为Ni，这Ni个个体中与Agent j相连的个数为Nij（Nij=Nji），那么Agent i对于Agent j的亲密程度hij表示如下：
值得注意的是，因为Ni≠Nj，所以hij≠hji。此外，为便于计算，本章假设网络中所有个体的连接均为双向连接。
（2）友善度gij
当Agent i与Agent j进行交互时，由于二者之间的态度值存在差异，两者交互所获得的收益不同。个体通常会更多地向意见相近者表示善意，这与余弦函数在［0，π］区间内单调递减的趋势相近，即态度距离
越大，其友善度越低，当差值介于某个阈值内时，友善度为正，在到达阈值后，友善度减小为负值，并随着态度距离的增加而继续减小。而本章假设态度值处于［-1，1］区间内，态度距离
则位于［0，2］区间，因此本章乘以系数
用以限定值域取值范围。基于此，gij的计算如下：
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
