个体动态从众性对网络群体行为的影响

本章提出个体动态从众性的概念，认为随着网络中所有个体态度偏离程度的降低，开始形成主流态度之后，Agent i对于自身观点的自信程度会受到社会主流舆情的影响，从而更倾向于听从他人意见，具体表现为公式（6-13）—公式（6-17）。为验证其实用性及有效性，仿真实验分别验证动态从众性与静态从众性对舆情极化的影响，进而揭示极化现象产生的机理。

根据公式（6-14）与公式（6-15）所表示的动态从众性函数ζi（t），在t=0时刻，Agent i的从众性ζi（0）=1-Yi，因此在静态从众性的公式中，所有时刻Agent i的从众性都为1-Yi，如公式（6-18）和公式（6-19）所示。基于可视化考虑，Yi取值为0.6，结果如图6-2—图6-7所示。

图6-2　静态从众性下舆情演化图

图6-3　静态从众性下极化概率图

图6-4　静态从众性下不同时刻观点分布直方图

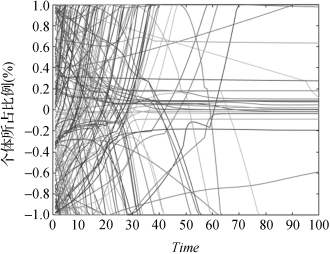
图6-5　动态从众性下舆情演化图

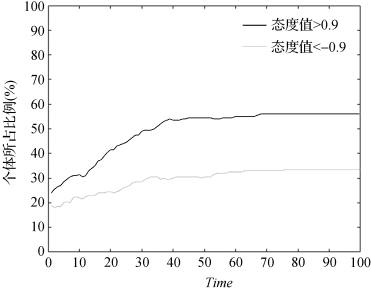
图6-6　动态从众性下极化概率图

(www.xing528.com)

图6-7　动态从众性下不同时刻观点分布直方图

图6-2与图6-5分别表示静态从众性及动态从众性下个体舆情演化情况；图6-3与图6-6分别表示在上述两种情况下网络中观点接近极化状态的个体占全部个体的比重的极化程度；图6-4与图6-7分别表示在上述两种情况下不同时间段网络中观点分布情况。由图6-2、图6-3、图6-4所示的静态从众性下的仿真结果可知，在Time=10时除少数中立个体外，其余个体基本上已经形成了极化，并且这些个体形成极化的时间非常接近；而与此相对应，如图6-5、图6-6、图6-7所示的动态从众性下，在Time=30时才初步形成极化效果，但其极化程度明显大于前者。这说明，只有在充分交互后形成的观点才更具持久性，在现实中个体只有在自身观点充分得到表达，并且搜集到足够多的信息之后，观点才不会再改变。因此，本章模型更加符合现实，同时，研究动态从众性有助于揭示极化演进机理，甚至对极化过程进行干预。

动态从众性函数ζi（t）中的重要参数固有自信度Yi对于极化有着至关重要的影响，代表着Agent i在初始时刻，完成交互时对于自身观点的认可度，从而影响从众性大小。为研究Yi对于极化的影响，本部分将Yi分别设定为0.2，0.4，0.6，0.8这4个不同的值进行仿真，观察不同Yi取值下出现观点极化的个体占全部个体的比例，结果如图6-8所示。

图6-8　不同固有自信度Yi下极化概率图

由图6-8可知，网络中所有Agent在进行充分交互后，出现观点极化的个体所占比例与固有自信度Yi有关。本次仿真设置初始时刻社会平均态度T（0）=0，当Yi值较小时，由于“沉默螺旋”效应，个体对于自身观点不够自信，容易出现强势观点碾压另一方的现象；而随着Yi增大，强势观点的强度减弱，渐渐地，两种极化程度势均力敌。

此外，除固有自信度参数Yi外，本章在公式（6-12）中定义社会从众性影响参数μ为倾向于和社会主流态度Π（t）一致的概率。为分析参数μ对极化现象的影响，本部分将μ设定为0.2，0.4，0.6，0.8，在保持其余变量相同的情况下观察这4个取值下的个体舆情演化有何不同，结果如图6-9和图6-10所示。图6-9表示4种不同μ取值下各舆情演化情况，图6-10表示4种不同μ取值下网络中出现观点极化的个体占全部个体的比例用以表述网络的个体观点极化程度，极化概率情况。

图6-9　不同μ取值下舆情演化图

图6-10　不同μ取值下极化概率图

由图6-9和图6-10可知，随着社会从众性影响参数μ的增大，网络中个体观点演化的时间逐渐增加。当μ=0.2时，在time=10的情况下，极化率不再变化；当μ=0.4时，则延迟到Time=15；当μ=0.6时，则需要Time=30；而图6-10（d）中，当μ=0.8时，极化率则在Time=50后还在上升。与此相对应的是，当网络中的态度值不再演化时，网络中极化个体的比例也不再有明显变化。由此可知，当个体偏向于与社会主流态度一致时，个体会花费更多的时间搜集信息，因此极化的进程会减慢，但是即使极化的速度有所减慢，最终网络中的极化率也不会变化。