基于热红外图像的人体目标识别方法

本节探讨一种基于相位一致性特征（phase congruency based feature，PCF）和相关向量机（RVM）的人体目标识别方法［120］。

1）相位一致性的定义

设为图像I（x）第s尺度，第o方向上的偶对称和奇对称滤波器。该滤波器组在I（x）上的响应为

其中，“*”表示卷积运算。由此可得在图像位置x处的响应幅度Aso和相角φso分别为

于是可定义图像位置x处的相位一致性（phase congruency，PC）为［60］

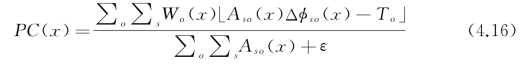
其中，Wo（x）为sigmoid函数，To为第o方向上的噪声能量估计，ε为避免除零错误的常数，Δφso为相位偏差。Δφso（x）的定义为

其中，为第o方向上的平均相角。

2）相位一致性特征

考虑Log-Gabor小波滤波特性与人体视觉特性良好的一致性，选择Log-Gabor小波滤波器组作为令｛G（fs，θo）∶s=1，2，…，p；o=1，2，…，q｝表示第s尺度，第o方向上的Log-Gabor滤波器对，其数学表达式为

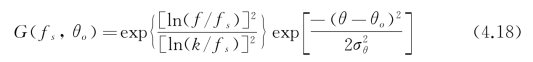
其中，f和θ表示G（fs，θo）在频域中的极坐标，k为沿半径方向的带宽，θo为滤波器方向，σθ为控制角度带宽的参数。这些参数可按如下方式确定：

由此可定义第o方向上的相位一致性为

将全部q方向相位一致性按逐点方式比较取最大，可得最大相位一致性为

现将PCo（x）划分为M×N个不相互重叠的网格，之后计算各网格内所有点的灰度均值，再将所得均值按之字形扫描顺序合并形成中间向量

对PCmax（x）进行同样的处理可以得到中间向量

最后将上述中间向量Ho，o=1，2，…，q以及Hmax串并，形成相位一致性特征向量，即

相位一致性计算示例如图4.11所示。

图4.11　相位一致性计算示例

（a）人体ROI；（b）～（g）6个方向的PCo；（h）PCmax

3）RVM的数学描述

RVM是一种基于贝叶斯推理学习的核机器学习方法。它与SVM一样具有稀疏解，从而在对新数据进行预测时只依赖于在训练数据的一个子集上计算的核函数，这个子集称为相关向量（relevance vector）。通过引入贝叶斯方法，RVM可以提供测试样本的后验概率输出且能产生更稀疏的解。RVM的分类性能与SVM相近甚至更好，而稀疏性通常远优于SVM，尤其当训练样本集规模较大时，优势更为明显，因此RVM比SVM更适于解决大训练样本集下的在线分类问题。(www.xing528.com)

现对RVM的工作原理加以理论说明［121-122］。

令为一组训练样本，t=为对应的类别标签，N为样本数。RVM定义如下分类函数

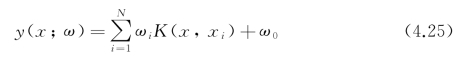
其中，ωi为模型权值，K（x，xi）为核函数。对y（x；ω）应用Sigmoid函数σ（y）=1/（1+e-y），使得p（t|x）服从Bernoulli分布。假设训练集样本独立同分布，则训练样本集的似然函数为

其中，t=（t1，t2，…，tN）T，ω=（ω0，ω1，…，ωN）T。

在贝叶斯框架下，可以通过最大似然估计对ω进行求解，但为防止模型存在过多的相关向量，避免过拟合，提高泛化能力，为权值ω定义高斯先验概率分布：

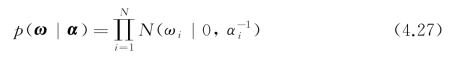
其中，α=（α0，α1，…，αN）为N+1维超参数，并假设α服从Gamma先验概率分布。由贝叶斯理论，可得

因p（ω|t，α）∝p（t|ω）p（ω|α），所以对ω的最大后验概率估计可等价为最大化：

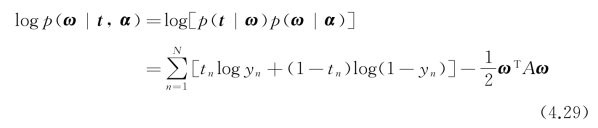
其中，A=diag（α0，α1，…，αN），yn=σ｛y（xn；ω）｝。

又p（α|t）∝p（t|α）p（α），所以p（α|t）的求解可转化为对p（t|α）的最大化，即

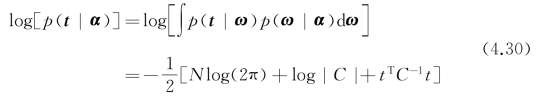
通过迭代求解式（4.29）和式（4.30），大部分ωi将趋于0，少量的ωi将趋于稳定的有限值，对应的xi为支持向量，实现模型稀疏化。

RVM分类决策准则为σ（yi）=1/（1+e-yi）＜0.5，则ti=0；反之，则ti=1，由此确定测试样本类别及其后验概率。

4）实验结果与讨论

对FLIR A40热像仪拍摄的一系列热红外序列图像进行图像分割后得到6 000余个候选目标，从中人工挑选具有代表性的人体目标与非人体目标各280个构成测试数据集，用于测试本节算法。数据集中的部分代表性样本如图4.12所示。

图4.12　测试数据集中的部分代表性样本

设定Log-Gabor小波尺度p=1，方向数q在［1，8］内变化，划分非重叠网格的方式从2×2到6×6变化。然后从测试样本集上提取PCF，结合RVM进行人体目标/非人体目标识别。RVM分类器使用高斯核函数，核函数带宽参数使用5折交叉验证精度（cross validation accuracy，CVA）进行优化。随机抽取数据集中80%样本用于RVM训练，余下20%样本用于测试，重复十次后计算CVA，结果列于表4.1。由表中数据可见本节算法的识别精度在多数情况下能够达到90%以上，具有较好的识别性能；其次，方向数q在6以内时，识别精度大致上随着方向数q变大而提高，表明人体轮廓具有有限的方向，因而可确定Log-Gabor滤波器的最优方向数（在这里为6）；最后，在中等粒度网格划分下，例如4×4、5×5，识别精度高于其他粒度网格划分方式，说明过粗的网格尺寸不能足够好地表达主要边缘信息，而过小的网格尺寸则对噪声敏感，因此综合计算效率考虑，采用4×4网格最优。

表4.1　不同参数设置下本节算法的CVA值

取上述优化参数值，将PCF与HOG［106］、最大方向能量直方图（histogram of maximal oriented energy，HMOE）［123］进行性能对比（均结合使用RVM）。对比测试中，用于RVM训练的样本比例从50%变化到80%。测试结果示于表4.2和图4.13。表4.2显示采用50%样本训练RVM后，PCF获得91.96%的CVA值，比HMOE和HOG分别高2%和6%。采用80%样本训练RVM后，PCF获得96.52%的CVA值，比HMOE和HOG高5%左右。图4.13进一步显示了在这两种训练样本占比下分类器的ROC曲线，可见对应于PCF的ROC曲线AUC值均高于其他两种对比特征，体现了PCF特征的优越性和RVM较强的泛化性能。

表4.2　PCF与HOG、HMOE的CVA和AUC指标对比

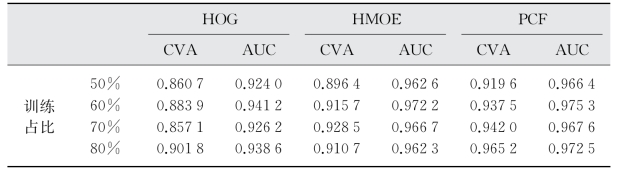
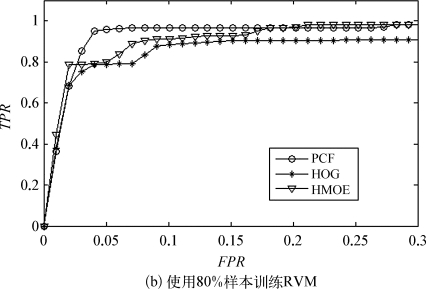
图4.13　PCF、HOG、HMOE特征对应的ROC曲线

综上，本节方法构建的PCF利用了相位一致性不受图像亮度/对比度变化影响的优点，实现了对热红外图像中人体边缘信息的良好表达，结合利用RVM优越的分类性能，获得了比典型传统方法更好的热红外人体目标识别性能。