基于热红外图像的人体目标检测方法成果

LSAC模型的三个要素是模型建立、水平集表达和数值算法。模型建立是确定活动轮廓曲线的演化方程，它是LSAC模型实现图像分割的依据。水平集表达是将活动轮廓曲线用水平集函数的零水平集隐式表示。数值算法用于求解关于活动轮廓曲线的演化方程，确定曲线在图像上的最终位置（该位置对应图像分割结果），而求解过程对应曲线在图像定义域上的演化过程（包含位移、变形、分裂合并等）。对模型要素的不同配置，决定了模型精度、效率、鲁棒性等性能的好坏。

1）面向热红外图像特点的LSAC模型的建立方法

第一类方法是基于图像边缘信息建立LSAC模型。一般可采用气球力项和边缘停止项来控制活动轮廓曲线的运动。其中，气球力项使曲线收缩或扩展并使其在图像定义上移动。边缘停止项则基于梯度检测使曲线停止在期望的目标边界位置。这类模型的一般框架是

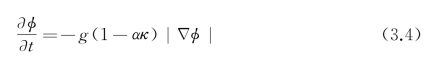
其中，φ为水平集函数，α为控制活动轮廓平滑度的常数，κ为曲率，g为边缘停止函数。当g值趋近于零时，曲线运动速度g（1-ακ）接近零，停止在图像中梯度值大的地方形成目标轮廓。这类模型对目标边缘定位准确度一般较高，但噪声及弱边缘会导致性能退化。另外，活动轮廓曲线的最终位置和它的初始位置密切相关。若初始位置选择不当，最终轮廓曲线对目标边缘的定位精度可能降低甚至完全无法使用。

第二类方法是构造能量泛函。能量泛函提供了一种高效灵活的框架，可以实现对图像边缘、区域、纹理、运动、数值约束等信息的综合利用。在能量泛函框架下，合理选择图像信息，并结合核函数映射、模糊集、贝叶斯概率分析等信息处理工具，可以设计出各具特色的LSAC模型。这里以C-V模型［74］、Salah模型［75］、局部二值拟合（local binary fitting，LBF）模型［76］为例加以说明。

C-V模型利用图像中目标/背景平均灰度这种全局性区域信息实现对弱边缘或无边缘图像目标的良好分割。对定义在图像域Ω上的图像函数I，C-V模型极小化如下能量泛函：

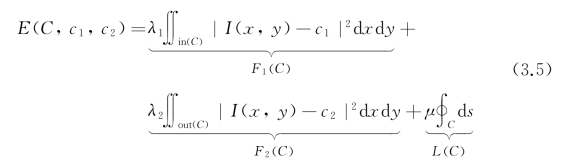
其中，L（C）为弧长正则项，用以消除演化过程中轮廓附近可能出现的小的虚假区域，并保证曲线演化的光滑性；F1（C）、F2（C）为全局能量项，其和反映了分割前和分割后图像的差异；c1、c2为曲线内部和外部区域的平均灰度，全局能量项使用它们达到近似图像I中位于曲线内和曲线外的区域的目的。

容易看出，C-V模型无法有效处理对比度很低的图像或非匀质性很强的图像。对比度低的图像中目标和背景的灰度均值十分接近，难以对活动轮廓曲线施加有效驱动使之运动到目标边缘。在非匀质性强的图像中，前景目标的灰度非常不均匀，平均灰度不是相应图像区域的有效表达。为此，Salah模型和LBF模型都分别基于核函数给出了解决方案。

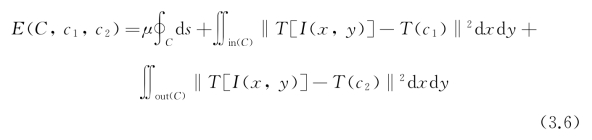
Salah模型定义的能量泛函如下：其中T为基于核函数［例如径向基函数（radial basis function，RBF）核］的非线性变换，作用是将数据从观测空间映射到高维特征空间。如图3.4所示，数据空间线性不可分的样本被变换到高维空间后变得线性可分，这样增强了模型分辨近似图像区域的能力。

图3.4　核函数映射改善样本可分性示意图［75］

LBF模型定义的能量泛函如下：

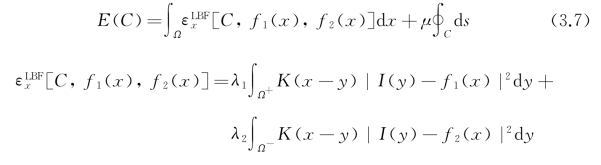
其中，I（y）是中心点x局部领域内的像素点y的灰度，f1（x）、f2（x）为用于近似x局部领域处的轮廓内区域Ω+和轮廓外区域Ω-的函数值。K∶Rn∈［0，+∞）满足：①K（-u）=K（u）；②若|u|＜|v|，则K（u）＞K（v），且lim|u|→+∞K（u）=0；③∫K（x）dx=1的核函数。借助核函数的局部化性质，通过极小化式（3.7），LBF较好地解决了非匀质图像的分割问题。

图3.5展示了上述模型在静态热红外图像上的分割效果。该图的顶行为三幅测试图像，叠加在图上的黑色曲线是初始轮廓曲线，其余各幅图像之上的黑色曲线为各模型输出的最终轮廓曲线，曲线所围成的区域为前景目标区域。三幅测试图像中，图3.5（a）的成像质量相对较好，对比度较高，人体区域和背景区域的灰度都比较均匀，各模型都较准确地分割出了图中人体目标。图3.5（b）的背景较均匀，但对比度变差，图像人体目标的灰度具有非匀质性，各模型对它的分割质量均明显变差。图3.5（c）的对比度很低，而且目标和背景灰度都非常不均匀，C-V模型和Salah模型对该图的分割完全失败，LBF表现相对较好，但分割出的人体目标不完整。

图3.5　C-V模型、Salah模型、LBF模型在静态热红外图像上的分割效果

（a）（b）（c）初始轮廓；（d）（e）（f）C-V模型分割结果；（g）（h）（i）Salah模型分割结果；（j）（k）（l）LBF模型分割结果

继续考察LSAC模型在红外序列图像上的分割效果。序列图像除具有静态图像的特点外还蕴含丰富的运动信息。基于这些运动信息，广大研究者从不同角度提出一些各具特色的LSAC模型。例如，Cremers et al.［77］和Lee et al.［78］给出了基于背景相减和帧差技术的LSAC模型。运用这两种方法分割测试序列图像，得到的代表性结果如图3.6和图3.7所示。图3.6显示Cremers et al.的方法错分了较多背景区域，且存在较严重的拖尾和目标破碎问题。类似地，图3.7也显示Lee et al.的方法也未能避免目标破碎问题。

图3.6　Cremers et al.的方法在热红外序列图像上的分割效果（第一行：序列1；第二行：序列2）

图3.7　Lee et al.的方法在热红外序列图像上的分割效果（第一行：序列1；第二行：序列2）

上述结果反映出现有LSAC模型在热红外图像上的适应性较差。首先，较强的图像噪声使得基于边缘信息建立的LSAC模型性能不理想。其次，热红外图像的低对比度特点使得目标与背景区域的灰度十分接近，两者间的灰度分界难以准确确定。再次，人体目标所具有的非匀质性及带辉光效应，使利用平均灰度等简单特征来近似人体区域不可行。因此，对于热红外图像中的人体目标分割问题，在构建新的LSAC模型时，综合利用包括梯度在内的多种信息，同时引入比平均灰度鉴别力更强的局部特征是合理可行的选择。

对于热红外序列图像，除具有静态红外图像的各种特征外，还存在背景运动、噪声变化等时域特征（或运动特征），因此需要细致考虑LSAC模型的建立方式。一方面，不同序列图像之间存在的显著差异使运动信息的提取技术存在差异；另一方面，时域和非时域方面的复杂特点相结合后，往往使基于纯运动信息的LSAC模型难以达到期望的分割质量。因此，将序列图像按其时域特征划分为多个类别是必要的，有利于指导相应LSAC模型的构建。(www.xing528.com)

2）高性能数值算法的开发

LSAC模型实现图像分割时，活动轮廓曲线从初始位置到终点目标边缘的运动过程，对应着对模型的数值求解过程。精度高、收敛快、稳定性好是对高性能数值算法的要求。

LSAC模型中，数值算法求解的对象通常为PDE，因为无论是直接基于曲线演化理论建立的LSF演化方程，还是基于能量泛函结合变分法获得的梯度下降流方程，都属于定义在连续域上的PDE。由于数字图像自然地构成等分网格，故定义在网格上的离散LSF可用于表示连续LSF，由此可实现对PDE的离散化。

（1）有限差分法。

有限差分法（Finite Difference Method，FDM）是求解离散化PDE的常用方法，其基本思想是利用相邻点函数值的差与它们之间距离的比值近似函数对变量的偏导数。通常，令τ为时间步长，（i，j）表示像素坐标，κτ为当前时刻，Δx、Δy分别为x和y方向上的网格宽度，则PDE中的时间导数可离散为

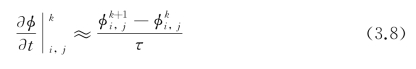
其中，空间导数通常有如下离散方式。

前向差分：

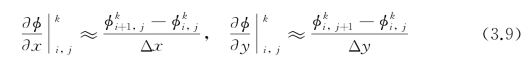
后向差分：

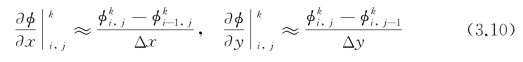
中心差分：

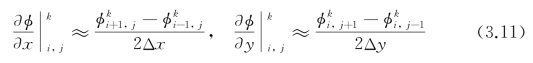
选择不同的离散形式，将φ关于时间和空间的导数全部离散后，PDE被转换为关于φk+1和φk的代数方程（或方程组）。方程（组）的格式有显式、隐式和半隐式。显式格式易于构造，但稳定性常需满足一定的约束条件。隐式格式稳定性高甚至无条件稳定，但求解过程涉及求解非线性方程组，计算复杂。相对而言，半隐式格式，例如Vese格式［74］、加性算子分裂格式（additional operator splitting，AOS）［79］等，因兼具前两者的优点而得到广泛使用。

（2）全局解凸性化方法。

近年来出现的几种获取全局解凸性化方法，例如全局凸分割（globally convex segmentation，GCS）方法［80］、全变分范数对偶格式（dual formulation of total variation norm，DFTVN）［81］、分裂Bregman方法［8283］等。GCS首先将非凸模型转化为带约束条件的凸模型，然后使用惩罚函数将其转换为无约束优化问题后求取全局解。DFTVN利用加权全变分范数向模型引入边缘信息，并采用与GCS类似的途径将模型转换为无约束优化问题，再构造对偶格式获得全局解。分裂Bregman方法则进一步解决了DFTVN方法求解效率随精度增加而降低的问题。

图3.8给出了显式差分格式、Vese半隐差分格式、AOS半隐差分格式、DFTVN格式求解的C-V模型分割三幅热红外图像（从左到右依次编号为1＃～3＃）的结果。其中，图3.8（a）叠加显示了前三种FDM格式的初始LSF（以黑色曲线表达其零水平集），图3.8（b）～（e）是各数值格式所得解（同样以其零水平集表达）。对比可看出各数值算法所得解的精度差异。此外，表3.1还列出了各数值算法在某PC机平台上的平均耗时，可见数值算法在极大程度上决定了LSAC模型的运行效率。

图3.8　采用不同数值方法实现的C-V模型在测试图像上的分割效果

表3.1　C-V模型在使用不同数值格式时分割测试图像的平均耗时

（3）窄带技术。

窄带技术［8485］是改善数值算法运行效率的一种重要技术手段。如图3.9所示，若活动轮廓C=｛φ=0｝某时刻的位置如图中黑实线所示，则在接下来的数值迭代中，窄带演化技术只更新其周围宽度为δ的窄带区域（该区域的内、外两侧边界为水平集｛φ=±δ/2｝）内的LSF值，从而使C在窄带内移动直到在某些位置碰到窄带边界（但始终不跨越边界），然后再在这些地方重构窄带，重复以上过程直到收敛。由于窄带区域内像素数目只是整个图像域像素数目的一小部分，这样迭代过程中需计算LSF值的点的数目极大减少，从而节约大量计算时间。当然，窄带宽度会限制C在每次迭代过程中的最大移动距离为δ/2，可能导致迭代次数增加。

图3.9　在水平集｛φ＝0｝附近宽度为δ的窄带

许多红外人体目标检测系统对运行效率提出了严格要求，这要求LSAC模型应具有计算复杂度低、收敛速度快的特点。然而，上述测试反映出一些常用的数值计算方法不能满足此要求，因此需要对数值算法从LSF函数选择、数值迭代效率、稳定性等方面着力改进。